Bài 1
Viết số hoặc tỉ số vào chỗ chấm:
a)
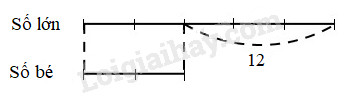
Hiệu của hai số bằng ….
Số lớn được biểu thị là … phần bằng nhau.
Số bé được biểu thị là …. phần như thế.
Tỉ số của số lớn và số bé là ..........
Hiệu số phần bằng nhau là … phần.
b)
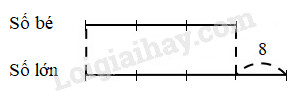
Hiệu của hai số bằng …
Số bé được biểu thị là … phần bằng nhau.
Số lớn được biểu thị là …. phần như thế.
Tỉ số của số bé và số lớn là …
Hiệu số phần bằng nhau là … phần.
Phương pháp giải:
Quan sát sơ đồ để hoàn thành bài tập đã cho.
Lời giải chi tiết:
a) Tóm tắt:
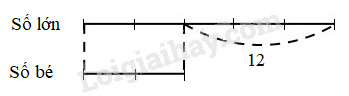
Hiệu của hai số bằng 12.
Số lớn được biểu thị là 5 phần bằng nhau.
Số bé được biểu thị là 2 phần như thế.
Tỉ số của số lớn và số bé là 5 : 2 hay \(\displaystyle {5 \over 2}\)
Hiếu số phần bằng nhau là 3 phần.
b) Tóm tắt:
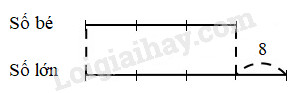
Hiệu của hai số bằng 8.
Số bé được biểu thị là 3 phần bằng nhau.
Số lớn được biểu thị là 4 phần như thế.
Tỉ số của số bé và số lớn là 3 : 4 hay \(\displaystyle {3 \over 4}\)
Hiệu số phần bằng nhau là 1 phần.
Bài 2
Hiệu hai số là 34. Tỉ số của hai số đó là \(\displaystyle{5 \over 3}\). Tìm hai số đó.
Phương pháp giải:
1. Tìm hiệu số phần bằng nhau.
2. Tìm giá trị của 1 phần bằng cách lấy hiệu hai số chia cho hiệu số phần bằng nhau.
3. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).
4. Tìm số lớn (lấy số bé cộng với hiệu của hai số ...).
Chú ý: Bước 2 và bước 3 có thể gộp lại thành một bước; có thể tìm số lớn trước rồi tìm số bé sau.
Lời giải chi tiết:
Ta có sơ đồ :
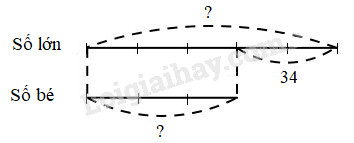
Theo sơ đồ, hiệu số phần bằng nhau:
5 – 3 = 2 (phần)
Số lớn là :
34 : 2 × 5 = 85
Số bé là:
85 – 34 = 51
Đáp số : Số lớn : 85 ;
Số bé : 51.
Bài 3
Đoạn đường AB ngắn hơn đoạn đường CD là 2km. Tìm chiều dài mỗi đoạn đường đó, biết rằng chiều dài của đoạn thẳng AB bằng \(\displaystyle {3 \over 4}\) chiều dài đoạn thẳng CD.
Lời giải chi tiết:
Ta có sơ đồ :
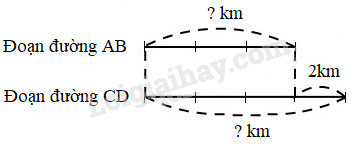
Theo sơ đồ, hiệu số phần bằng nhau là :
4 – 3 = 1 (phần)
Chiều dài đoạn đường AB là:
2 : 1 × 3 = 6 (km)
Chiều dài đoạn đường CD là:
6 + 2 = 8 (km)
Đáp số: Đoạn đường AB : 6km ;
Đoạn đường CD : 8km.
dapandethi.vn
