Phần 1
Khoanh tròn vào chữ đặt trước câu trả lời đúng.
1. Trong các số 6215; 6261; 617 ; 6281 số chia hết cho 3 là :
A. 6215 B. 6261 C. 6217 D. 6281
Phương pháp giải:
Tính tổng các chữ số của các số đã cho.
Số có tổng các chữ số chia hết cho 3 thì chia hết cho 3.
Giải chi tiết :
Trong các số đã cho, số chia hết cho 3 là 6261.
Chọn B.
2. Hòa có 8 viên bi gồm 4 viên màu xanh , 3 viên bi màu đỏ, 1 viên bi màu vàng. Phân số chỉ phần các viên bi màu xanh trong tổng số viên bi của Hòa là:
A. \(\displaystyle{4 \over 3}\) B. \(\displaystyle{3 \over 8}\) C. \(\displaystyle{1 \over 8}\) D. \(\displaystyle{4 \over 8}\)
Phương pháp giải:
Phân số chỉ các viên bi màu đỏ trong số viên bi của Hùng có tử số là số viên bi màu đỏ, mẫu số là tổng số viên bi của Hùng.
Giải chi tiết :
Phân số chỉ các viên bi màu xanh trong số viên bi của Hòa là \( \displaystyle{4 \over 8}\).
Chọn D.
3. Phân số \(\dfrac{7}{8}\) bằng phân số:
A. \(\displaystyle{{21} \over {32}}\) B. \(\displaystyle{{35} \over {32}}\) C. \(\displaystyle{{21} \over {24}}\) D. \(\displaystyle{{35} \over {48}}\)
Phương pháp giải:
Áp dụng tính chất cơ bản của phân số : Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác \(0\) thì được một phân số mới bằng phân số đã cho.
Giải chi tiết :
Ta có :
\(\dfrac{7}{8}=\dfrac{7\times 3}{8 \times 3}=\dfrac{21}{24} \)
Vậy trong các phân số đã cho, phân số bằng \(\dfrac{7}{8}\) là \(\dfrac{21}{24}.\)
Chọn C.
4. Trong các phân số phân số bé hơn 1 là:
A. \(\displaystyle{8 \over 7}\) B. \(\displaystyle{7 \over 7}\) C. \(\displaystyle{8 \over 8}\) D. \(\displaystyle{7 \over 8}\)
Phương pháp giải:
Phân số có tử số bé hơn mẫu số thì phân số đó bé hơn 1.
Giải chi tiết :
Trong các phân số đã cho, phân só bé hơn 1 là \( \displaystyle{7 \over 8}\).
Chọn D
Phần 2
1. Đặt tính rồi tính:
\(78653 + 80694\) \(527684 – 81946\)
\(526 \times 205\) \(76140 : 324\)
Phương pháp giải:
Đặt tính rồi tính theo các quy tắc đã học về phép cộng, trừ, nhân, chia các số tự nhiên.
Giải chi tiết :

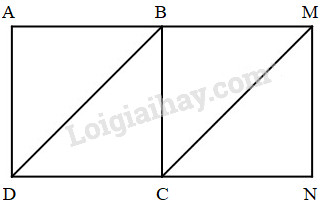
2. Hai hình vuông ABCD và BMNC đều có cạnh bằng 3cm và xếp thành hình chữ nhật AMND. Cho biết hình tứ giác BMCD là hình bình hành. Tính diện tích hình bình hành BMCD bằng các cách khác nhau.
Phương pháp giải:
- Áp dụng các công thức :
+ Diện tích hình bình hành = độ dài đáy × chiều cao tương ứng.
+ Diện tích hình vuông = cạnh × cạnh.
* Cách 1 : Diện tích hình bình hành BMCD = DC × BC : 2.
* Cách 2 : Diện tích hình bình hành BMCD = Diện tích nửa hình vuông ABCD + Diện tích nửa hình vuông BMNC.
Giải chi tiết :
Cách 1:
Hình vuông ABCD có cạnh = 3 cm nên DC = BC = 3 cm.
Diện tích hình bình hành BMCD là:
DC × BC = 3 × 3 = 9 (cm2)
Đáp số: 9cm2.
Cách 2:
Diện tích hình bình hành BMCD bằng diện tích nửa hình vuông ABCD + diện tích nửa hình vuông BMNC.
Diện tích nửa hình vuông ABCD có cạnh bằng 3 cm là:
(3 × 3) : 2 = 4,5 (cm2)
Diện tích nửa hình vuông BMNC có cạnh bằng 3cm là:
(3 × 3) : 2 = 4,5 (cm2)
Diện tích hình bình hành BMCD là:
4,5 + 4,5 = 9 (cm2)
Đáp số: 9cm2.
dapandethi.vn