Bài 1
Viết tỉ số vào ô trống :
|
a |
3 |
2m |
4kg |
3\(l\) |
4 giờ |
\(1{m^2}\) |
|
b |
8 |
5m |
9kg |
7\(l\) |
5 giờ |
\(3{m^2}\) |
|
Tỉ số của a và b |
|
|
|
|
|
|
|
Tỉ số của b và a |
|
|
|
|
|
|
Phương pháp giải:
Áp dụng định nghĩa : Tỉ số của \(a\) và \(b\) là \(a: b\) hay \(\dfrac{a}{b}\) (\(b\) khác \(0\)).
Lời giải chi tiết:
|
a |
3 |
2m |
4kg |
3\(\displaystyle l\) |
4 giờ |
\(\displaystyle 1{m^2}\) |
|
b |
8 |
5m |
9kg |
7\(\displaystyle l\) |
5 giờ |
\(\displaystyle 3{m^2}\) |
|
Tỉ số của a và b |
\(\displaystyle {3 \over 8}\) |
\(\displaystyle {2 \over 5}\) |
\(\displaystyle {4 \over 9}\) |
\(\displaystyle {3 \over 7}\) |
\(\displaystyle {4 \over 5}\) |
\(\displaystyle {1 \over 3}\) |
|
Tỉ số của b và a |
\(\displaystyle {8 \over 3}\) |
\(\displaystyle {5 \over 2}\) |
\(\displaystyle {9 \over 4}\) |
\(\displaystyle {7 \over 3}\) |
\(\displaystyle {5 \over 4}\) |
\(\displaystyle {3 \over 1}\) |
Bài 2
Hai túi gạo cân nặng 54kg. Túi thứ nhất cân nặng bằng \(\displaystyle {4 \over 5}\) túi thứ hai. Hỏi mỗi túi cân nặng bao nhiêu ki-lô-gam gạo ?
Phương pháp giải:
1. Vẽ sơ đồ: coi số gạo của túi thứ nhất (đóng vai trò số bé) gồm 4 phần bằng nhau thì số gạo của túi thứ hai (đóng vai trò số lớn) gồm 5 phần như thế.
2. Tìm tổng số phần bằng nhau.
3. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau.
4. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).
5. Tìm số lớn (lấy giá trị một phần nhân với số phần của số lớn hoặc lấy tổng hai số trừ đi số bé).
Chú ý: Bước 3 và bước 4 có thể gộp lại thành một bước.
Lời giải chi tiết:
Ta có sơ đồ :
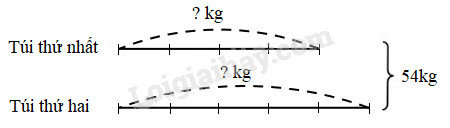
Theo sơ đồ, tổng số phần bằng nhau là :
4 + 5 = 9 (phần)
Túi thứ nhất cân nặng số ki-lô-gam gạo là:
54 : 9 × 4 = 24 (kg)
Túi thứ hai cân nặng số ki-lô-gam gạo là:
54 – 24 = 30 (kg)
Đáp số: Túi thứ nhất : 24kg ;
Túi thứ hai : 30kg.
Bài 3
Viết số thích hợp vào ô trống :
|
Tổng |
360 |
392 |
1692 |
11 256 |
|
Tỉ số |
1 : 7 |
5 : 9 |
19 : 17 |
123 : 45 |
|
Số thứ nhất |
|
|
|
|
|
Số thứ hai |
|
|
|
|
Phương pháp giải:
Tìm hai số theo bài toán tìm hai số khi biết tổng và tỉ số của hai số đó.
Lời giải chi tiết:
|
Tổng |
360 |
392 |
1692 |
11 256 |
|
Tỉ số |
1 : 7 |
5 : 9 |
19 : 17 |
123 : 45 |
|
Số thứ nhất |
45 |
140 |
893 |
8241 |
|
Số thứ hai |
315 |
252 |
799 |
3015 |
Bài 4
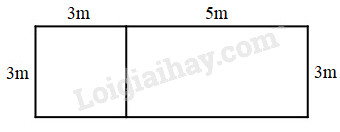
Hình vuông có cạnh là 3m. Hình chữ nhật có chiều rộng là 3m và chiều dài là 5m. Tìm tỉ số của diện tích hình vuông và diện tích hình chữ nhật.
Phương pháp giải:
- Tìm diện tích các hình theo các công thức :
+) Diện tích hình vuông = cạnh × cạnh.
+) Diện tích hình chữ nhật = chiều dài × chiều rộng.
- Tìm tỉ số diện tích hai hình dựa vào định nghĩa : Tỉ số của \(a\) và \(b\) là \(a: b\) hay \(\dfrac{a}{b}\) (\(b\) khác \(0\)).
Lời giải chi tiết:
Diện tích hình vuông là:
\(3 \times 3 = 9\;({m^2})\)
Diện tích hình chữ nhật là:
\(5 \times 3 = 15\;({m^2})\)
Tỉ số diện tích hình vuông và hình chữ nhật là :
\(9 : 15\) hay \( \displaystyle {9 \over {15}}\) hay \(\displaystyle{3 \over 5}\)
Đáp số: \(9:15\) hay \(\displaystyle{3 \over 5}.\)
dapandethi.vn
