Bài 1
Đánh dấu (x) vào ô trống đặt dưới hình thoi có diện tích bé hơn \(20cm^2\).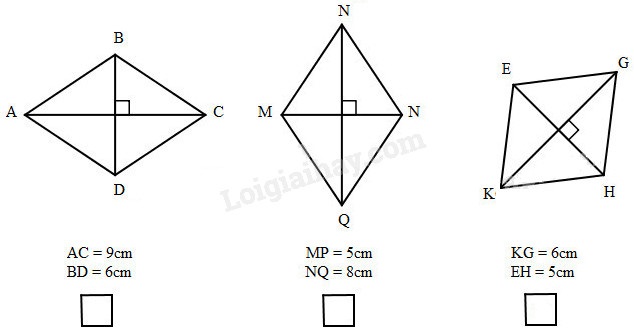
Phương pháp giải:
- Tính diện tích các hình thoi rồi so sánh kết quả với \(20cm^2.\)
- Diện tích hình thoi bằng tích của độ dài hai đường chéo chia cho 2 (cùng đơn vị)
\(S = {\displaystyle {m \times n} \over 2}\) hoặc \( S = m \times n : 2\)
(\(S\) là diện tích của hình thoi, \(m, n\) là độ dài của hai đường chéo).
Lời giải chi tiết:
Diện tích hình thoi ABCD là:
\( \displaystyle{{9 \times 6} \over 2} =27\left( {c{m^2}} \right) > 20cm^2\)
Diện tích hình thoi MNPQ là :
\( \displaystyle{{8 \times 5} \over 2} = 20\left( {c{m^2}} \right)\)
Diện tích hình thoi EGHK là :
\( \displaystyle{{6 \times 5} \over 2} = 15\left( {c{m^2}} \right) < 20cm^2\)
Vậy ta có kết quả như sau :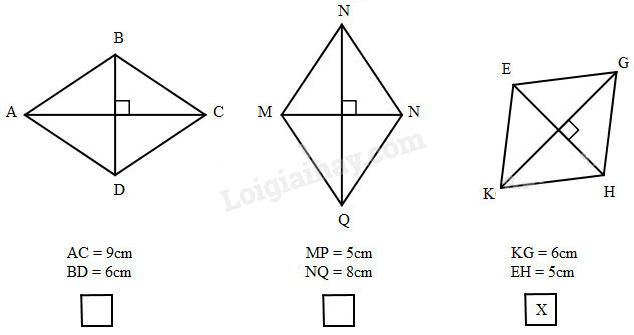
Bài 2
Viết vào ô trống :
|
Hình thoi |
(1) |
(2) |
(3) |
|
Đường chéo |
12cm |
16dm |
20m |
|
Đường chéo |
7cm |
27dm |
5m |
|
Diện tích |
|
|
|
Phương pháp giải:
Áp dụng quy tắc : Diện tích hình thoi bằng tích của độ dài hai đường chéo chia cho 2 (cùng đơn vị đo).
Lời giải chi tiết:
|
Hình thoi |
(1) |
(2) |
(3) |
|
Đường chéo |
12cm |
16dm |
20m |
|
Đường chéo |
7cm |
27dm |
5m |
|
Diện tích |
42cm2 |
216dm2 |
50m2 |
Bài 3
Một mảnh bìa hình thoi có độ dài đường chéo là 10cm và 24cm. Tính diện tích mảnh bìa đó.
Phương pháp giải:
Muốn tính diện tích của mảnh bìa ta lấy tích của độ dài hai đường chéo chia cho 2 (cùng đơn vị đo).
Lời giải chi tiết:
Diện tích của mảnh bìa là:
\(\displaystyle {{10 \times 24} \over 2} = 120\;(cm^2)\)
Đáp số: \(120cm^2.\)
dapandethi.vn
