Bài 1
Video hướng dẫn giải
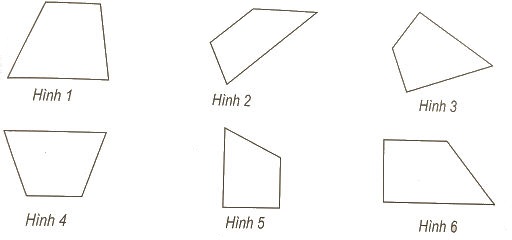
Trong các hình dưới đây, hình nào là hình thang:
Phương pháp giải:
Áp dụng tính chất: Hình thang có một cặp cạnh đối diện song song.
Lời giải chi tiết:
Quan sát hình vẽ ta thấy: hình 1, hình 2, hình 4, hình 5, hình 6 là hình thang.
Bài 2
Video hướng dẫn giải
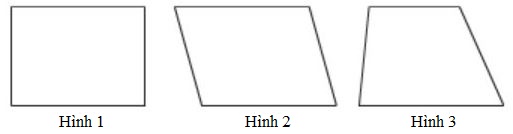
Trong ba hình dưới đây, hình nào có:
- Bốn cạnh và bốn góc ?
- Hai cặp cạnh đối diện song song ?
- Chỉ có một cặp cạnh đối diện song song ?
- Có bốn góc vuông ?
Phương pháp giải:
Quan sát hình vẽ để trả lời các câu hỏi.
Lời giải chi tiết:
- Hình 1, hình 2, hình 3, mỗi hình đều có bốn cạnh và bốn góc.
- Hình 1, hình 2, mỗi hình có hai cặp cạnh đối diện song song.
- Hình 3 chỉ có một cặp cạnh đối diện song song.
- Hình 1 có bốn góc vuông.
Bài 3
Video hướng dẫn giải
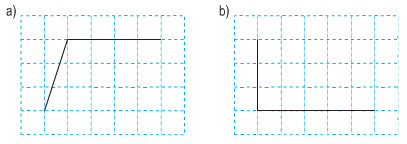
Vẽ thêm hai đoạn thẳng vào mỗi hình dưới đây để được hình thang:
Phương pháp giải:
Sử dụng tính chất: hình thang có một cặp cạnh đối diện song song.
Lời giải chi tiết:
Có thể vẽ thêm vào mỗi hình hai đoạn thẳng như sau:
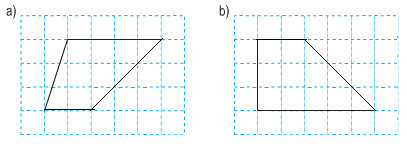
Lưu ý: có nhiều cách vẽ thêm hai đoạn thẳng vào mỗi hình đã cho để được hình thang, học sinh tùy chọn cách phù hợp.
Bài 4
Video hướng dẫn giải
Hình thang ABCD có những góc nào là góc vuông ? Cạnh bên nào vuông góc với hai đáy ?
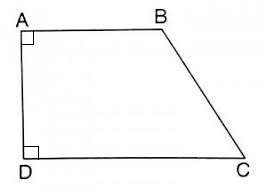
Hình thang có một cạnh bên vuông góc với hai đáy gọi là hình thang vuông.
Phương pháp giải:
Quan sát hình vẽ để trả lời câu hỏi.
Lời giải chi tiết:
Hình thang ABCD có góc A và góc D là góc vuông.
Cạnh bên AD vuông góc với hai đáy.
Nói thêm : cạnh bên AD là đường cao của hình thang vuông ABCD.
dapandethi.vn
Lý thuyết
Diện tích hình tam giác
Quy tắc: Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho $2$.
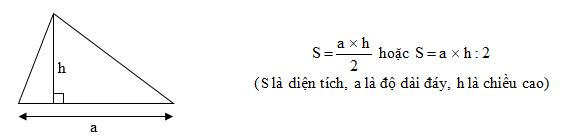
Chú ý: Muốn tính diện tích tam giác vuông ta lấy độ dài hai cạnh góc vuông nhân với nhau (cùng một đơn vị đo) rồi chia cho \(2\).
Ví dụ 1: Tính diện tích hình tam giác có độ dài đáy là \(13cm\) và chiều cao là \(8cm\).
Cách giải:
Diện tích hình tam giác đó là:
\(13 \times 8:2 = 52(c{m^2})\)
Đáp số: \(52c{m^2}\).
Ví dụ 2: Tính diện tích hình tam giác có độ dài đáy là \(2m\) và chiều cao là \(15dm\).
Cách giải:
Đổi \(2m = 20dm\)
Diện tích hình tam giác đó là:
\(20 \times 15:2 = 150(d{m^2})\)
Đáp số: \(150c{m^2}\).
3) Một số dạng bài tập
Dạng 1: Tính diện tích tam giác khi biết độ dài đáy và chiều cao
Phương pháp: Áp dụng công thức: \(S = \dfrac{{a\,\, \times \,\,h}}{2}\) hoặc \(S = a\,\, \times \,\,h:2\)
(\(S\) là diện tích, \(a\) là độ dài đáy, \(h\) là chiều cao)
Dạng 2: Tính độ dài đáy khi biết diện tích và chiều cao
Phương pháp: Từ công thức tính diện tích \(S = \dfrac{{a\,\, \times \,\,h}}{2}\) hoặc \(S = a\,\, \times \,\,h:2\), ta có công thức tính độ dài đáy như sau: \(a = \dfrac{{S \times 2}}{h}\) hoặc \(a = S \times 2:h\).
Dạng 3: Tính chiều cao khi biết diện tích và độ dài đáy
Phương pháp: Từ công thức tính diện tích \(S = \dfrac{{a\,\, \times \,\,h}}{2}\) hoặc \(S = a\,\, \times \,\,h:2\), ta có công thức tính chiều cao như sau: \(h = \dfrac{{S \times 2}}{a}\) hoặc \(h = S \times 2:a\).
Dạng 4: Toán có lời văn
Phương pháp: Đọc kĩ đề bài, xác định dạng toán trong bài rồi giải bài toán đó.
