Đề bài
Bài 1. Cho hình vuông ABCD, M là trung điểm của CD, N là trung điểm của AD. Gọi I là giao điểm của AM và BN.
Chứng minh rằng: \({S_{DMIN}} = {S_{AIB}}.\)
Bài 2. Cho hình chữ nhật ABCD, E là điểm tùy ý trên AB.
Chứng minh rằng: \({S_{ABCD}} = 2{S_{EDC}}.\)
Phương pháp giải - Xem chi tiết
Sử dụng: Hai tam giác bằng nhau có diện tích bằng nhau.
Lời giải chi tiết
Bài 1.
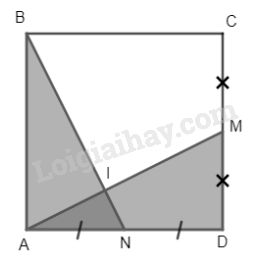
Ta có: \(AB=AD,AN=MD\) (do ABCD là hình vuông) và \(\widehat A =\widehat D=90^0\) (do ABCD là hình vuông)
Suy ra \(\Delta BAN = \Delta ADM\left( {c.g.c} \right)\)
\( \Rightarrow {S_{BAN}} = {S_{ADM}}\)
\( \Rightarrow {S_{BAN}} - {S_{AIN}} = {S_{ADM}} - {S_{AIN}}\)
Hay \({S_{AIB}} = {S_{DMIN}}.\)
Bài 2.
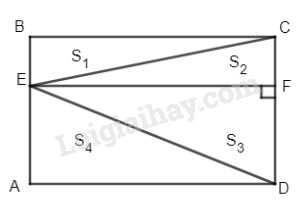
Kẻ \(EF \bot CD\) ta có BCFE và EFDA là các hình chữ nhật
Suy ra \(\Delta BCE = \Delta FEC\left( {c.g.c} \right)\) , tương tự \(\Delta AED = \Delta FDE.\)
Do đó (theo hình vẽ):
\({S_1} = {S_2}\) và \({S_3} = {S_4}\)
\( \Rightarrow {S_1} + {S_3} = {S_1} + {S_4} = {1 \over 2}{S_{ABCD}}\)
Hay \({S_{ECD}} = {1 \over 2}{S_{ABCD}} \Rightarrow {S_{ABCD}} = 2{S_{ECD}}.\)
dapandethi.vn
