Đề bài
Cho hình chữ nhật ABCD, E là điểm tùy ý trên cạnh AB. Chứng minh rằng: \({S_{ABCD}} = 2{S_{EDC}}.\)
Phương pháp giải - Xem chi tiết
Hai tam giác bằng nhau có diện tích bằng nhau.
Diện tích tam giác bằng nửa tích chiều cao với cạnh đáy.
Lời giải chi tiết
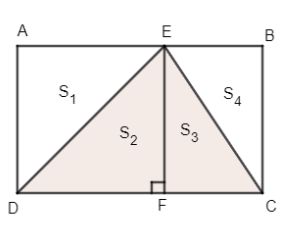
Kẻ \({\rm{EF}} \bot DC\) ta có AEFD, EBCF là các hình chữ nhật (vì có 3 góc vuông)
Suy ra AD=EF, AE=DF, \(\widehat A = \widehat F =90^0\)
Do đó \(\Delta DAE = \Delta {\rm{EFD}}\left( {c.g.c} \right)\)
Tương tự \(\Delta EBC = \Delta CFE.\)
Gọi \({S_1},{S_2},{S_3},{S_4}\) lần lượt là diện tích các tam giác (theo hình vẽ), ta có
\({S_1} = {S_2};{S_3} = {S_4}\)
Suy ra \({S_1} + {S_2}+{S_3} + {S_4}=2(S_2+S_3)\)
Hay \({S_{ABCD}} = 2{S_{EDC}}.\)
dapandethi.vn
