Đề bài
Cho hình vuông ABCD có cạnh a, giao điểm hai đường chéo là O. Một góc vuông \(\widehat {xOy}\) sao cho Ox cắt cạnh AB tại E, tia Oy cắt cạnh BC tại F.
Tính \({S_{OEBF}}\) theo a.
Phương pháp giải - Xem chi tiết
Sử dụng:
Các tam giác bằng nhau có diện tích bằng nhau
Diện tích hình vuông bằng bình phương 1 cạnh
Lời giải chi tiết
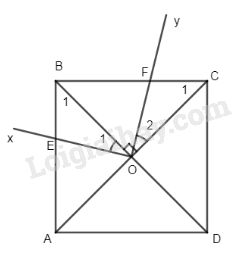
Ta có: \({S_{OEBF}} = {S_{OEB}} + {S_{OFB}}.\)
Nối O với A, B. Xét \(\Delta OEB\) và a\(\Delta OFC\)có:
\(\widehat {{B_1}} = \widehat {{C_1}} = {45^ \circ },\)
OB = OC,
\(\widehat {{O_1}} = \widehat {{O_2}}\) (cùng phụ với \(\widehat {{\rm{BOF}}}\)).
\( \Rightarrow \Delta OEB = \Delta OFC\left( {g.c.g} \right)\)
Do đó: \({S_{OEBF}} = {S_{OFC}} + {S_{OFB}} = {S_{OBC}} \)\(\,=\dfrac {1}{ 4}{S_{ABCD}} = {1 \over 4}{a^2}.\)
dapandethi.vn
