Đề bài
Cho đa giác n – cạnh có diện tích S, các đường thẳng a, b, c cắt nhau tại A, B, C nằm trong tam giác sao cho mỗi đường thẳng chia đa giác thành hai phần có diện tích bằng nhau.
Chứng minh rằng \({S_{ABC}} \le \dfrac{1}{4}S.\)
Phương pháp giải - Xem chi tiết
Phân chia đa giác thành các tam giác để so sánh.
Lời giải chi tiết
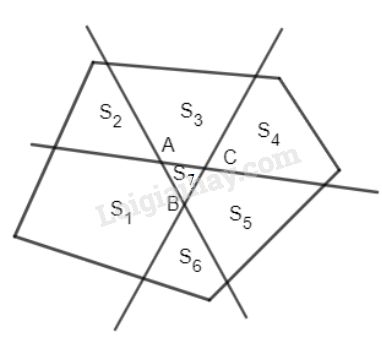
Gọi diện tích của các phần của đa giác được chia bởi các đường thẳng là \({S_1},\,{S_2},{S_3},...\)
Ta có: \({S_1} + {S_2} + {S_6} = \dfrac{1}{2}S = {S_1} + {S_6} + {S_5} + {S_7}\)
\( \Rightarrow {S_2} = {S_5} + {S_7}\) mà \(\dfrac{1 }{ 2}S = {S_1} + {S_2} + {S_3} + {S_7}\)
\( \Rightarrow {1 \over 2}S = {S_1} + {S_5} + {S_7} + {S_3} + {S_7} > 2{S_7}\)
\(\Rightarrow {S_7} < \dfrac{1 }{ 4}S.\)
Vậy \({S_{ABC}} < \dfrac{1 }{4}S\) (đpcm).
dapandethi.vn
