Đề bài
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm củ các cạnh AB, BC, CD và DA
a) Chứng minh: tứ giác MNPQ là hình bình hành.
b) Chứng minh: \({S_{MNPQ}} = \dfrac{1}{2}{S_{ABCD.}}\)
Phương pháp giải - Xem chi tiết
Sử dụng:
Tứ giác có cặp cạnh đối song song và bằng nhau là hình bình hành
Diện tích tam giác bằng nửa tích đường cao với cạnh đáy tương ứng
Lời giải chi tiết
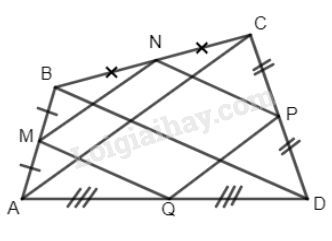
a) Ta có MN là đường trung bình của \(\Delta ABC\)
\( \Rightarrow MN// AC\) và \(MN = {1 \over 2}AC\)
Tương tự \(QP//AC\) và \(QP = {1 \over 2}AC\)
Do đó \(MN// QP\) và MN = QP
Vậy tứ giác MNPQ là hình bình hành.
b) Ta có: \({S_{BMN}} = \dfrac{1 }{ 4}{S_{ABC}}\) (do chiều cao hạ từ đỉnh B của tam giác ABC gấp 2 lần chiều cao hạ từ B của tam giác BMN và đáy AC=2MN)
Tương tự: \({S_{DPQ}} = \dfrac{1 }{4}{S_{ACD}}\)
\( \Rightarrow {S_{BMN}} + {S_{DPQ}} = \dfrac{1 }{ 4}\left( {{S_{ABC}} + {S_{ACD}}} \right) \)\(\,= \dfrac{1 }{ 4}{S_{ABCD.}}\)
Tương tự \({S_{CNP}} + {S_{AMQ}} = \dfrac{1 }{4}{S_{ABCD}}\)
Do đó: \({S_{BMN}} + {S_{DQP}} + {S_{CNP}} + {S_{AMQ}} \)\(\,= \dfrac{1}{2}{S_{ABCD}}.\)
Vậy: \({S_{MNPQ}} = \dfrac{1 }{ 2}{S_{ABCD.}}\)
dapandethi.vn
