Đề bài
Cho hình chữ nhật ABCD. Lấy E, F, G, H lần lượt trên các cạnh AB, BC, CD sao cho tứ giác EFGH có hai đường chéo EG và FH vuông góc với nhau. Chứng minh: \({S_{EFGH}} \ge {1 \over 2}{S_{ABCD}}.\)
Phương pháp giải - Xem chi tiết
Sử dụng:
Tứ giác có hai đường chéo vuông góc với nhau có diện tích bằng nửa tích hai đường chéo
Lời giải chi tiết
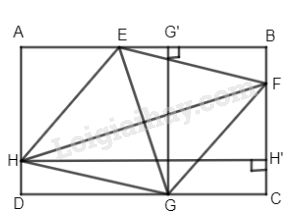
Gọi \(H'\) là hình chiếu của H trên BC và \(G'\) là hình chiếu của G trên AB.
Ta có: \({S_{EFGH}} = {1 \over 2}EG.HF\)
Và \({S_{ABCD}} = AD.CD;\)
\(EG \ge GG' = AD;\)
\(HF \ge HH' = CD.\)
Do đó: \({S_{EFGH}} \ge \dfrac{1}{ 2}{S_{ABCD}}.\)
dapandethi.vn
