Đề bài
Cho tam giác ABC, lấy P, Q lần lượt là trung điểm cạnh AB và AC. Kẻ BE, CF cùng vuông góc với PQ.
a)Chứng minh tứ giác BCFE là hình chữ nhật.
b)Chứng minh \({S_{BCFE}} = {S_{ABC}}.\)
Phương pháp giải - Xem chi tiết
Sử dụng:
Tứ giác có cặp cạnh đối song song và bằng nhau là hình bình hành
Hình bình hành có 1 góc vuông là hình chữ nhật
Các tam giác bằng nhau có diện tích bằng nhau
Lời giải chi tiết
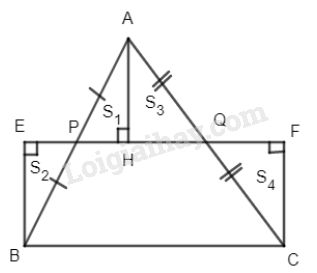
a) Ta có PQ là đường trung bình của \(\Delta ABC\) nên \(PQ// BC.\)
Lại có \(BE// CF\left( { \bot PQ} \right)\) nên BCFE là hình bình hành có một góc vuông.
Do đó BCFE là hình chữ nhật.
b) Kẻ \(AH \bot PQ.\) Ta có \(\Delta AHP = \Delta BEP\) (ch-gn)
Tương tự \(\Delta AHQ = \Delta CFQ\) (ch-gn)
Gọi \({S_1},{S_2},{S_3},{S_4}\) lần lượt là diện tích các tam giác AHP, BEP, AHQ và CFQ.
Ta có: \({S_1} = {S_2}\) và \({S_3} = {S_4}\)
Mà \({S_{BCEF}} = {S_2} + {S_{BPQC}} + {S_4}\) và \({S_{ABC}} = {S_1} + {S_{BPQC}} + {S_3}.\)
Do đó: \({S_{BCEF}} = {S_{ABC}}\).
dapandethi.vn
