Đề bài
Cho hình bình hành ABCD. Trên tia đối của tia BC lấy điểm E sao cho BE = BC. Trên tia đối của DC lấy điểm F sao cho DF = CD. Chứng minh rằng:
a) Tứ giác EBDA là hình bình hành.
b) Ba điểm E, A, F thẳng hàng
Phương pháp giải - Xem chi tiết
Sử dụng:
Trong hình bình hành, hai cạnh đối song song và bằng nhau.
Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
Lời giải chi tiết
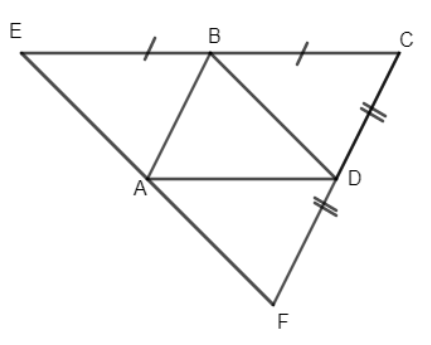
a) Vì ABCD là hình bình hành nên \(AD=BC\) mà \(BE=BC\) (gt) nên \(EB=AD\)
Ta có \(EB// AD\) và EB = AD nên EBDA là hình bình hành.
b) Ta có \(EA//BD\) (do EBDA là hình bình hành)
Vì ABCD là hình bình hành nên \(AB=DC\) mà \(DF=DC\) (gt) nên \(AB=DF\)
Ta có \(AB// FD\) và AB = FD nên ABDF là hình bình hành.
\( \Rightarrow AF// BD\)
Theo tiên đề Ơ- clit thì AE và AF phải trùng nhau hay ba điểm E, A, F thẳng hàng.
dapandethi.vn
