Đề bài
Cho tam giác ABC, hai trung tuyến BM, CN cắt nhau tại G. Gọi E, F lần lượt là trung điểm của GB và GC.
a) Chứng minh tứ giác MNEF là hình bình hành.
b) Lấy I, J thuộc tia đối của MG và NG sao cho MI = MG và NI = NG. Chứng minh tứ giác BCIJ là hình bình hành.
Phương pháp giải - Xem chi tiết
Sử dụng:
+) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Lời giải chi tiết
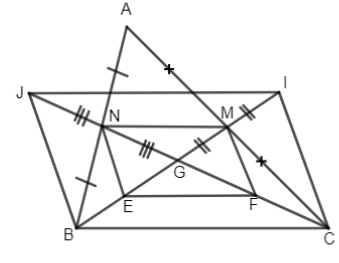
a) Ta có MN là đường trung bình của \(\Delta ABC\)
\( \Rightarrow MN//BC\) và \(MN = \dfrac{1}{ 2}BC.\)
Lại có EF là đường trung bình của \(\Delta BGC\) nên \({\rm{EF}}// BC\) và \({\rm{EF}} = \dfrac{1}{ 2}BC.\)
Do đó \(MN// {\rm{EF}}\) và \(MN = EF.\)
Vậy MNEF là hình bình hanh (hai cạnh đối vừa song song vừa bằng nhau).
b) Tam giác ABC có hai trung tuyến BM, CN cắt nhau tại G
Nên G là trọng tâm của \(\Delta ABC\), do đó \(GN = \dfrac{1 }{ 2}GC\)
Mà GN = JN (gt) \( \Rightarrow GJ = GC.\)
Tương tự ta có \(GM = \dfrac{1 }{ 2}GB\) (do G là trọng tâm tam giác ABC) mà \(GM=MI\) (gt)
Suy ra GI = GB.
Vậy tứ giác BJIC là hình bình hành (hai đường chéo CJ và BI cắt nhau tại trung điểm mỗi đường).
dapandethi.vn
