Đề bài
Cho hình bình hành ABCD \(\left( {AB > BC} \right)\), phân giác của góc D cắt AB tại M, phân giác của góc B cắt CD tại N.
a) Chứng minh rằng AM = CN.
b) Chứng minh: Tứ giác DMBN là hình bình hành.
Phương pháp giải - Xem chi tiết
Sử dụng: Tính chất hình bình hành và dấu hiệu tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
Lời giải chi tiết
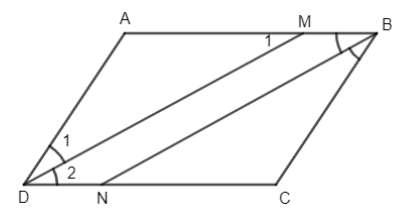
a) Vì ABCD là hình bình hành nên AB//CD
Ta có \(\widehat {{M_1}} = \widehat {{D_2}}\) (so le trong) mà \(\widehat {{D_2}} = \widehat {{D_1}}\) (do DM là phân giác góc ADC)
\( \Rightarrow \widehat {{M_1}} = \widehat {{D_1}}\) hay \(\Delta ADM\) cân \( \Rightarrow AM = AD.\)
Ta có \(\widehat {{ABN}} = \widehat {{BNC}}\) (so le trong) mà \(\widehat {{ABN}} = \widehat {{CBN}}\) (do BN là phân giác góc ABC)
\( \Rightarrow \widehat {{CBN}} = \widehat {{CNB}}\) hay \(\Delta BCN\) cân tại C
\( \Rightarrow CN = CB\) mà AD = CB (gt). Do đó AM = CN.
b) AB = CD (do ABCD là hình bình hành); AM = CN (cmt) \( \Rightarrow AB - AM = CD - CN\) hay BM = DN.
Lại có \(BM//DN.\) Do đó tứ giác DMBN là hình bình hành.
dapandethi.vn
