Đề bài
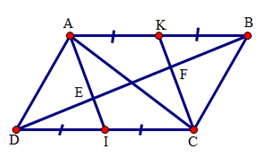
Cho hình bình hành \(ABCD\) . Gọi \(I,\text{ }K\) theo thứ tự là trung điểm của \(CD,\text{ }AB\) . Đường chéo \(BD\) cắt \(AI,\text{ }CK\) theo thứ tự ở \(E,\text{ }F\). Chứng minh rằng \(DE= FE= FB\)
Phương pháp giải - Xem chi tiết
Chứng minh tứ giác \(AKCI\) là hình bình hành để suy ra \(AI\parallel CK\) . Sau đó sử dụng định lí đường trung bình của các tam giác \(\Delta DCF,\Delta ABE\) để suy ra điều phải chứng minh.
Lời giải chi tiết
Vì \(AK=\dfrac{AB}{2},IC=\dfrac{CD}{2}\) (gt) mà \(AB=CD\) (cạnh đối hình bình hành) nên \(AK=IC\) .
Vì \(AB\parallel CD(gt),K\in AB,I\in DC\Rightarrow AK\parallel IC\) .
Tứ giác \(AKCI\) có \(AK\parallel CI,AK=IC(cmt)\) nên là hình bình hành.
Suy ra \(AI\parallel CK\)
Mà \(E\in AI,F\in CK\Rightarrow EI\parallel CF,KF\parallel AE\)
Xét \(\Delta DCF\) có: \(DI=IC(gt),IE\parallel CF(cmt)\)\(\\Rightarrow ED=FE(1)\)
Xét \(\Delta ABE\) có: \(AK=KB(gt),KF\parallel AE(cmt)\)\(\Rightarrow EF=FB(2)\)
Từ (1) và (2) suy ra \(ED=FE=FB\)
dapandethi.vn