Đề bài
Cho tam giác ABC có trực tâm H, kẻ \(Bx \bot AB,Cy \bot AC.\) Gọi D là giao điểm của Bx và Cy.
a) Chứng minhh: BHCD là hình bình hành.
b) Gọi O là trung điểm của BC. Chứng minh H, O, D thẳng hàng.
Phương pháp giải - Xem chi tiết
Sử dụng:
Tứ giác có hai cặp cạnh đối song song là hình bình hành
Hai đường chéo của hình bình hành giao nhau tại trung điểm mỗi đường
Lời giải chi tiết
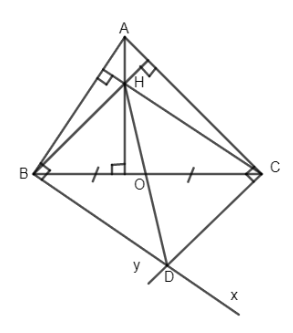
a) Ta có: \(Bx//CH( \bot AB)\)
Tương tự: \(Cy// BH( \bot AC)\)
Hay \(BD//CH\) và \(CD// BH.\)
Vậy tứ giác BHCD là hình bình hành.
b) Xét hình bình hành BHCD có O là trung điểm cuả BC \( \Rightarrow \) đường chéo thứ hai HD phải qua O.
Hay ba điểm H, O, D thẳng hàng.
dapandethi.vn
