Đề bài
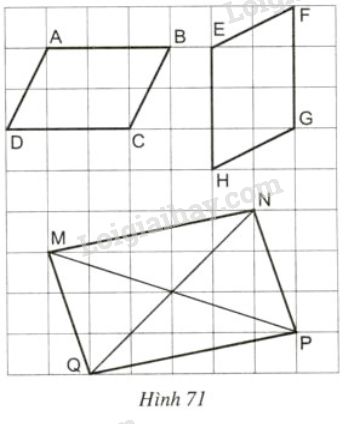
Các tứ giác \(ABCD, EFGH, MNPQ\) trên giấy kẻ ô vuông ở hình \(71\) có là hình bình hành hay không ?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng dấu hiệu nhận biết hình bình hành:
+) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+) Tứ giác có các cạnh đối bằng nhau là hình bình hành.
Lời giải chi tiết
Cả ba tứ giác đều là hình bình hành.
- Tứ giác \(ABCD\) là hình bình hành vì có:
\(AB // CD\) và \(AB = CD =3\) (Tứ giác có 2 cạnh đối song song và bằng nhau )
- Tứ giác \(EFGH\) là hình bình hành vì có:
\(EH // FG\) và \(EH = FG = 3\) (Tứ giác có 2 cạnh đối song song và bằng nhau )
- Tứ giác \(MNPQ\) có:
\(MN\) và \(PQ\) là cạnh huyền của tam giác vuông có hai cạnh góc vuông là \(1\) và \(5\).
Áp dụng định lí Py-ta-go ta có: \(MN = PQ = \sqrt {{5^2} + {1^2}} = \sqrt {26} \)
\(MQ\) và \(NP\) là cạnh huyền của tam giác vuông có hai cạnh góc vuông là \(1\) và \(3\)
Áp dụng định lí Py-ta-go ta có: \(MQ = NP = \sqrt {{3^2} + {1^2}} = \sqrt {10} \)
Do đó \(MNPQ\) là hình bình hành vì có \(MN = PQ\) và \(MQ = NP\) (Tứ giác có các cạnh đối bằng nhau).
dapandethi.vn
