Đề bài
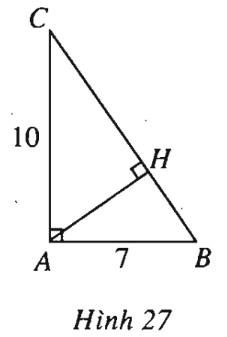
Tam giác \(ABC\) vuông ở \(A\) và có hai cạnh \(AB=7, AC=10.\)
a) Tìm cosin của các góc \(\left( {\overrightarrow {AB} \,,\overrightarrow {AC} \,} \right);\) \(\left( {\overrightarrow {AB} \,,\,\overrightarrow {BC} } \right)\,;\,\left( {\overrightarrow {AB} \,,\,\overrightarrow {CB} } \right)\,.\)
b) Gọi \(H\) là hình chiếu của \(A\) trên \(BC\). Tính \(\overrightarrow {HB} .\overrightarrow {HC} \).
Lời giải chi tiết
(h.27).
a) \((\overrightarrow {AB} ,\overrightarrow {AC} ) = {90^0}\) nên \(\cos (\overrightarrow {AB} ,\overrightarrow {AC} ) = 0\).
\((\overrightarrow {AB} ,\overrightarrow {BC} ) = {180^0} - \widehat {ABC}\) nên
\(\cos (\overrightarrow {AB} ,\overrightarrow {BC} ) = - \cos \widehat {ABC}\)
\(= - \dfrac{7}{{\sqrt {149} }}\).
\((\overrightarrow {AB} ,\overrightarrow {CB} ) = \widehat {ABC}\) nên \(\cos (\overrightarrow {AB} ,\overrightarrow {CB} ) = \dfrac{7}{{\sqrt {149} }}\).
b) \(\overrightarrow {HB} .\overrightarrow {HC} = HB.HC.\cos {180^0}\)
\(= - HB.HC = - A{H^2}.\)
Theo hệ thức trong tam giác vuông \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} = \dfrac{{149}}{{4900}}\), suy ra \(A{H^2} = \dfrac{{4900}}{{149}}\).
Vậy \(\overrightarrow {HB} .\overrightarrow {HC} = - \dfrac{{4900}}{{149}}\).
dapandethi.vn
