Đề bài
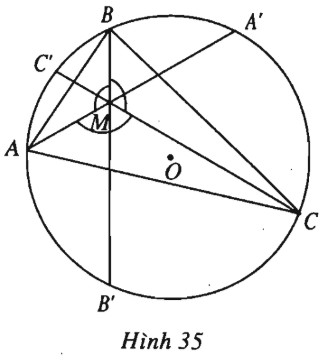
Cho tam giác \(ABC\) nội tiếp trong đường tròn \((O)\) và một điểm \(M\) sao cho các góc \(AMB, BMC, CMA\) đều bằng \(120^0\). Các đường thẳng \(AM, BM, CM\) cắt đường tròn \((O)\) lần lượt tại \(A’, B’, C’\). Chứng minh rằng:
\(MA+MB+MC\)\(=MA’+MB’+MC’.\)
Lời giải chi tiết
(h.35).
Lấy các điểm \(A_1, B_1, C_1\) sao cho \(\overrightarrow {M{A_1}} = \dfrac{{\overrightarrow {MA} }}{{MA}};\) \( \overrightarrow {M{B_1}} = \dfrac{{\overrightarrow {MB} }}{{MB}};\) \(\overrightarrow {M{C_1}} = \dfrac{{\overrightarrow {MC} }}{{MC}} \), khi đó cả ba vec tơ trên đều có độ dài bằng 1, mà góc giữa hai vectơ bất kì trong chúng đều bằng \(120^0\) nên \(M\) là tâm của tam giác đều \(A_1 B_1 C_1\).
Theo bài 24, ta có
\(2\overrightarrow {MA} .\overrightarrow {MO}\)
\( = MA(MA - MA')\), suy ra \(2\dfrac{{\overrightarrow {MA} }}{{MA}}.\overrightarrow {MO} \)
\(= MA - MA'\),
hay \(2\overrightarrow {M{A_1}} .\overrightarrow {MO} = MA - MA'\).
Tương tự
\(2\overrightarrow {M{B_1}} .\overrightarrow {MO} = MB - MB',\) \( 2\overrightarrow {M{C_1}} .\overrightarrow {MO} = MC - MC'.\)
Từ đó ta có
\(MA + MB + MC\)\( - MA' - MB' - MC' \)
\(= 2(\overrightarrow {M{A_1}} + \overrightarrow {M{B_1}} + \overrightarrow {M{C_1}} ).\overrightarrow {MO} = 0\)
Hay
\(MA + MB + MC\)\( = MA' + MB' + MC'\)
dapandethi.vn
