Đề bài
Tam giác \(ABC\) có các cạnh \(AC=b, AB=c\), \(\widehat {BAC} = \alpha \) và \(AD\) là phân giác của góc \(BAC\) (\(D\) thuộc cạnh \(BC\)).
a) Hãy biểu thị vec tơ \(\overrightarrow {AD} \)qua hai vec tơ \(\overrightarrow {AB} , \overrightarrow {AC} \).
b) Tính độ dài đoạn \(AD.\)
Lời giải chi tiết
(h.29).
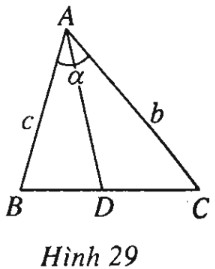
a) Theo tính chất của đường phân giác, ta có \(\dfrac{{DB}}{{DC}} = \dfrac{c}{b}\) hay \(DB = \dfrac{c}{b}DC\).
Mặt khác \(\overrightarrow {DB} , \overrightarrow {DC} \) ngược hướng nên \(\overrightarrow {DB} = - \dfrac{c}{b}\overrightarrow {DC} \). Từ đó dẫn đến
\(\overrightarrow {AB} - \overrightarrow {AD} = - \dfrac{c}{b}\left( {\overrightarrow {AC} - \overrightarrow {AD} } \right)\)\( \Leftrightarrow \left( {1 + \dfrac{c}{b}} \right)\overrightarrow {A{\rm{D}}} = \overrightarrow {AB} + \dfrac{c}{b}\overrightarrow {AC} \)\(\Leftrightarrow\overrightarrow {AD} = \dfrac{{b\overrightarrow {AB} + c\overrightarrow {AC} }}{{b + c}}.\)
b) Bình phương vô hướng để tính độ dài \(AD\). Ta có
\(AD = \dfrac{{bc}}{{b + c}}\sqrt {2(1 + \cos \alpha )} .\)
dapandethi.vn
