Đề bài
Cho tam giác \(ABC\) có \(BC = 12cm\), \(\widehat B = 60^\circ ,\widehat C = 40^\circ .\) Tính:
a) Đường cao \(CH\) và cạnh \(AC;\)
b) Diện tích tam giác \(ABC.\)
Phương pháp giải - Xem chi tiết
Trong một tam giác vuông, mỗi cạnh góc vuông bằng: Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Suy ra cạnh huyền bằng cạnh góc vuông chia sin góc đồi hoặc chia cosin góc kề.
Lời giải chi tiết
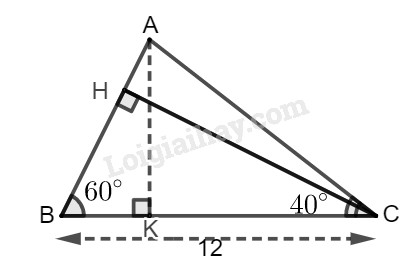
a) Trong tam giác vuông BCH, ta có:
\(CH = BC.\sin \widehat B\)\( = 12.\sin 60^\circ \approx 10,392\) (cm)
Trong tam giác ABC, ta có: \(\widehat {BAC} + \widehat B + \widehat {ACB} = {180^0}\) (tổng ba góc trong tam giác bằng \(180^0\))
Suy ra \(\widehat {BAC} = {180^0} - \left( {\widehat B + \widehat {ACB}} \right)\)\(= 180^\circ - (60^\circ + 40^\circ ) = 80^\circ \)
Trong tam giác vuông ACH, ta có:
\(AC = \dfrac{{CH}}{{\sin \widehat {HAC}}}\)\( \approx \dfrac{{10,392}}{{\sin 80^\circ }} = 10,552\) (cm)
b) Kẻ \(AK \bot BC\)
Trong tam giác vuông ACK, ta có:
\(AK = AC.\sin \widehat C\)\( \approx 10,552.\sin 40^\circ = 6,783\) (cm)
Vậy \({S_{ABC}} = \dfrac{1}{ 2}.AK.BC\)\( \approx \dfrac {1}{ 2}.6,783.12 = 40,698\) (cm2)
dapandethi.vn
