Đề bài
Cho tam giác \(ABC\) trong đó \(AB = 5cm, AC = 8cm\), \(\widehat {BAC} = 20^\circ \) . Tính diện tích tam giác \(ABC\), có thể dùng các thông tin dưới đây nếu cần:
\(\sin 20^\circ \approx 0,3420,\) \(cos20^\circ \approx 0,9397,\) \(tg20^\circ \approx 0,3640.\)
Phương pháp giải - Xem chi tiết
Cho hình vẽ:

Ta có: \(AB=BC. \sin \alpha \)
Sử dụng công thức tính diện tích tam giác bằng nửa tích chiều cao với cạnh đáy tương ứng.
Lời giải chi tiết
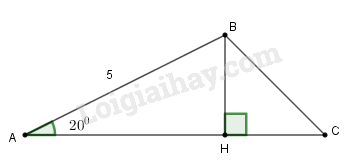
Kẻ \(BH \bot AC\) tại \(H\)
Trong tam giác vuông \(ABH\), ta có:
\(BH = AB.\sin \widehat A \)\(= 5.\sin 20^\circ \approx 1,7101\left( {cm} \right)\)
Ta có: \({S_{\Delta ABC}} = \dfrac{1}{2}BH.AC \)\(= \dfrac{1}{2}.8.1,7101 = 6,8404\left( {c{m^2}} \right)\)
dapandethi.vn
