Đề bài
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Biết \(HB = 25cm, HC = 64cm\). Tính \(\widehat B,\widehat C\).
Phương pháp giải - Xem chi tiết
Áp dụng hệ thức lượng trong tam giác \(ABC\) có đường cao \(AH\), ta có:
\(A{H^2} = BH.CH\)
Sử dụng tỉ số lượng giác của góc nhọn:

\(\tan \alpha = \dfrac{{AB}}{{AC}}.\)
Lời giải chi tiết
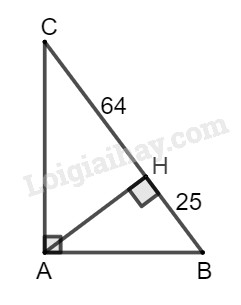
Xét tam giác ABC vuông tại A có chiều cao AH, theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
\(A{H^2} = HB.HC\)
Suy ra:
\(AH = \sqrt {HB.HC} = \sqrt {25.64} = \sqrt {1600} = 40\) (cm)
Trong tam giác vuông ABH, ta có:
\(tanB = \dfrac{{AH}}{{HB}} = \dfrac{{40}}{{25}} = 1,6\)
Suy ra:
\(\widehat B \approx 57^\circ 59'\)
Vì tam giác \(ABC\) vuông nên \(\widehat B + \widehat C = 90^\circ \)
Suy ra:
\(\widehat C = 90^\circ - \widehat B = 90^\circ - 57^\circ 59' = 32^\circ 1'\)
dapandethi.vn
