Đề bài
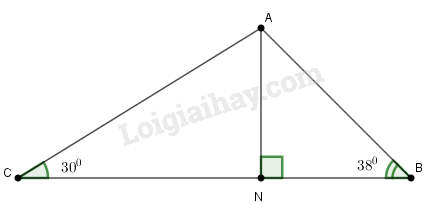
Trong tam giác \(ABC\) có \(AB = 11cm,\widehat {ABC} = 38^\circ ,\widehat {ACB} = 30^\circ \). \(N\) là chân đường vuông góc kẻ từ \(A\) đến \(BC\). Hãy tính \(AN, AC.\)
Phương pháp giải - Xem chi tiết
Cho hình vẽ:

Ta có: \(\sin \alpha = \dfrac{{AB}}{{BC}}\) nên \(AB=BC.\sin \alpha\) và \(BC = \dfrac{{AB}}{{\sin \alpha }}\)
Lời giải chi tiết
Trong tam giác vuông \(ABN\), ta có:
\(AN = AB.\sin \widehat B = 11.\sin 38^\circ \)\( \approx 6,772\left( {cm} \right)\)
Trong tam giác vuông \(ACN\), ta có:
\(AC = \dfrac{{AN}}{{\sin \widehat C}} \)\(\approx \dfrac{{6,772}}{{\sin 30^\circ }} = 13,544\left( {cm} \right)\)
dapandethi.vn
