Đề bài
Cho \(BCD\) là tam giác đều cạnh \(5cm\) và góc \(DBA\) bằng \(70^\circ \).
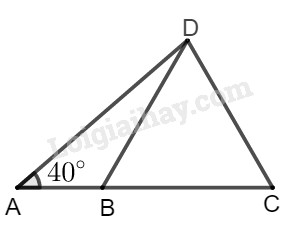
Hãy tính:
a) \(AD;\)
b) \(AB.\)
Phương pháp giải - Xem chi tiết
Cho hình vẽ:

Ta có: \(\sin \alpha = \dfrac{{AB}}{{BC}}\) nên \(AB=BC.\sin \alpha , \) \(BC = \dfrac{{AB}}{{\sin \alpha }}\) và \(\cot \alpha = \dfrac{{AC}}{{AB}}.\)
Lời giải chi tiết
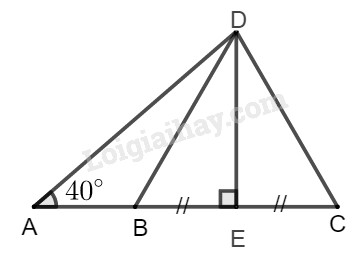
a) Kẻ \(DE \bot BC\)
Suy ra: \(BE = EC = \dfrac{1}{2}BC = 2,5\left( {cm} \right)\)
Trong tam giác vuông \(BDE\), ta có:
\(DE = BD.\sin \widehat {DBE}\)\( = 5.\sin 60^\circ = \dfrac{{5\sqrt 3 }}{2}\left( {cm} \right)\)
Trong tam giác vuông \(ADE\), ta có:
\(AD = \dfrac{{DE}}{{\sin \widehat A}} = \dfrac{{\dfrac{{5\sqrt 3 }}{2}}}{{\sin 40^\circ }}\)\( \approx 6,736\left( {cm} \right)\)
b) Trong tam giác vuông \(ADE\), ta có:
\(AE = AD.\cot g\ A \)\(\approx 6,736.\cot 40^\circ = 5,16\left( {cm} \right)\)
Ta có: \(AB = AE - BE\)\( = 5,16 - 2,5 = 2,66\left( {cm} \right)\)
dapandethi.vn
