Đề bài
Các cạnh của một tam giác có độ dài \(4cm, 6cm\) và \(6cm.\) Hãy tính góc nhỏ nhất của tam giác đó.
Phương pháp giải - Xem chi tiết
Sử dụng tính chất tam giác cân và tỉ số lượng giác của góc nhọn.
Cho tam giác \(ABC\) vuông tại \(A\) thì \(\sin B=\dfrac{AC}{BC}\)
Lời giải chi tiết
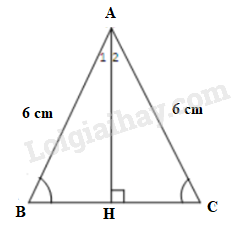
Vì các cạnh của tam giác lần lượt là \(4cm, 6cm\) và \(6cm\) nên tam giác đó là tam giác cân. Góc nhỏ nhất của tam giác là góc đối diện với cạnh \(4cm.\)
Giả sử tam giác \(ABC\) cân tại \(A\) có cạnh bên \(AB=AC=6cm\) và cạnh đáy \(BC=4cm.\) Ta tính góc \(BAC\)
Kẻ đường cao \(AH\bot BC\) tại \(H\)
Vì tam giác \(ABC\) cân nên đường cao \(AH\) vừa là đường trung tuyến vừa là đường phân giác.
Suy ra \(H\) là trung điểm của \(BC\) nên \(BH=HC=BC:2=2cm\)
Xét tam giác \(AHC\) vuông tại \(H,\) theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:
\(\sin \widehat {{A_2}} = \dfrac{{HC}}{{AC}} = \dfrac{2}{6} = \dfrac{1}{3}\)
Suy ra \(\widehat {{A_2}} \approx {19^0}28'\)
Mà \(AH\) là phân giác góc \(A\) (cmt) nên \(\widehat {BAC} = 2.\widehat {{A_2}} = {2.19^0}28' = {38^0}56'\)
Vậy góc nhỏ nhất của tam giác bằng \(38^\circ 56'\).
dapandethi.vn
