Đề bài
Tìm \(x\) và \(y\) trong các hình sau:
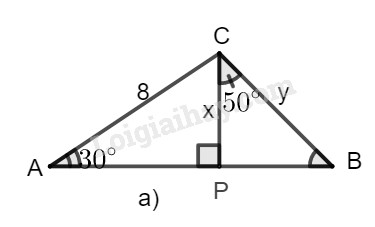
a)
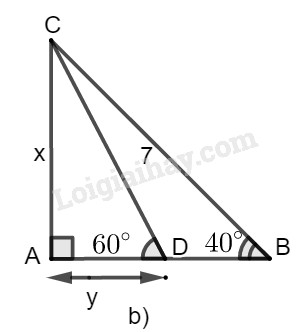
b)
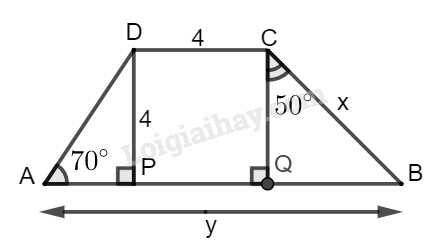
c)
Phương pháp giải - Xem chi tiết
+) Cho hình vẽ:

Ta có \(AB=BC.\sin \alpha, \) \(AC=AB. \cot \alpha\), \(BC = \dfrac{{AC}}{{\cos \alpha }}\)
+) Định lí Pytago vào tam giác \(ABC\) vuông tại \(A\):
\(A{B^2} + A{C^2} = B{C^2}.\)
Lời giải chi tiết
a) Hình a
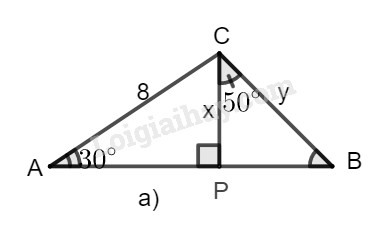
Trong tam giác vuông \(ACP\), ta có:
\(x = CP = AC.\sin \widehat A\)
\( = 8.\sin 30^\circ = 8.\dfrac{1}{2} = 4\)
Trong tam giác vuông BCP, ta có:
\(y = BC = \dfrac{x}{{\cos \widehat {BCP}}}\)\( = \dfrac{4}{{{\rm{cos50}}^\circ }} \approx 6,223\)
b) Hình b
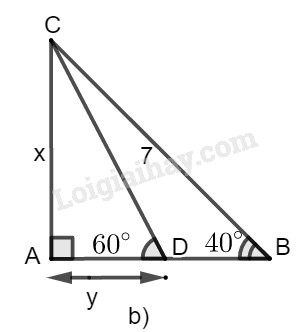
Trong tam giác vuông \(ABC\), ta có:
\(x = AC = BC.\sin \widehat B\)
\( = 7.\sin 40^\circ \approx 4,5\)
Trong tam giác vuông \(ACD\), ta có:
\(y = AD = AC.\cot \widehat D\)
\( \approx 4,5\cot 60^\circ \approx 2,598\)
c) Hình c
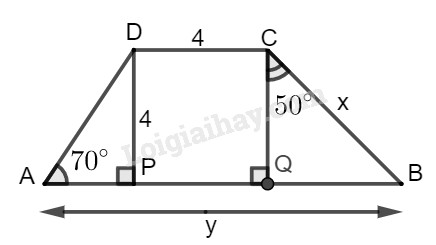
Vì tứ giác \(CDPQ\) có \(DC//PQ\), \(DP//CQ\) (vì cùng vuông với AB) nên \(CDPQ\) là hình bình hành có \(\widehat {DPQ} = {90^0}\) nên là hình chữ nhật. Mà \(CD = DP = 4\) nên \(CDPQ\) là hình vuông.
Suy ra: \(CD = DP = PQ = QC = 4\)
Trong tam giác vuông \(BCQ\), ta có:
\(x = BC = \dfrac{{CQ}}{{{\rm{cos}}\widehat {BCQ}}}\)\( = \dfrac{4}{{{\rm{cos50}}^\circ }} \approx 6,223\)
\(BQ = BC.\sin \widehat {BCQ}\)\( \approx 6,223.\sin 50^\circ \approx 4,767\)
Trong tam giác vuông \(ADP\), ta có:
\(AP = DP.\cot A \)\(= 4.\cot 70^\circ \approx 1,456\)
Ta có:
\(y = AB = AP + PQ + QB\)
\(= 1,456 + 4 + 4,767 = 10,223\).
dapandethi.vn
