Đề bài
Cho tam giác \(ABC\). Gọi \(A’\) là điểm đối xứng với \(B\) qua \(A, B’\) là điểm đối xứng với \(C\) qua \(B, C’\) là điểm đối xứng với \(A\) qua \(C\). Chứng minh rằng với một điểm \(O\) bất kì, ta có:
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} \)\( = \overrightarrow {OA'} + \overrightarrow {OB'} + \overrightarrow {OC'} \).
Lời giải chi tiết
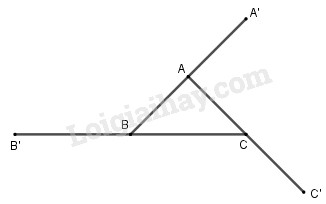
Ta có
\(\eqalign{ & \,\,\,\,\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} \cr & = \overrightarrow {OA'} + \overrightarrow {A'A} + \overrightarrow {OB'} + \overrightarrow {B'B} + \overrightarrow {OC'} + \overrightarrow {C'C} \cr & = \overrightarrow {OA'} + \overrightarrow {AB} +\overrightarrow {OB'} +\overrightarrow {BC} + \overrightarrow {OC'} + \overrightarrow {CA} \cr & = (\overrightarrow {OA'} + \overrightarrow {OB'} + \overrightarrow {OC'} ) + \left( {\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} } \right) \cr} \)
\(= \overrightarrow {OA'} + \overrightarrow {OB'} + \overrightarrow {OC'} +\overrightarrow {0}\)
\(= \overrightarrow {OA'} + \overrightarrow {OB'} + \overrightarrow {OC'} \)
dapandethi.vn
