Đề bài
Cho tam giác OAB. Giả sử \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OM} ,\) \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {ON} \). Khi nào điểm \(M\) nằm trên đường phân giác của góc \(AOB\)? Khi nào điểm \(N\) nằm trên đường phân giác ngoài của góc \(AOB\)?
Phương pháp giải - Xem chi tiết
Sử dụng quy tắc hình bình hành và điều kiện điểm M để suy ra OAMB là hình thoi.
Sử dụng tính chất đường phân giác trong và đường phân giác ngoài vuông góc để suy ra OM vuông góc ON.
Từ đó suy ra OAMB là hình thoi.
Lời giải chi tiết
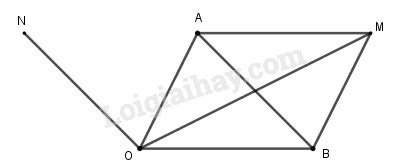
Ta có: \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OM} \) nên OAMB là hình bình hành
M nằm trên đường phân giác trong góc AOB nên OM là phân giác trong góc AOB
\( \Rightarrow OAMB\) là hình thoi
\( \Rightarrow OA = OB\).
Lại có, \(\overrightarrow {ON} = \overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} \) nên \(ON//BA\).
N nằm trên đường phân giác ngoài của hóc AOB \( \Leftrightarrow OM \bot ON\)
\( \Rightarrow OM \bot BA\)
\( \Rightarrow OAMB\) là hình thoi.
Vậy \(OA = OB\).
dapandethi.vn
