Đề bài
Cho hình ngũ giác đều \(ABCDE\) tâm \(O\). Chứng minh rằng
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {OE} = \overrightarrow 0 \).
Hãy phát biểu bài toán trong trường hợp n-giác đều.
Phương pháp giải - Xem chi tiết
Viết \(\overrightarrow u = \overrightarrow {OA} + (\overrightarrow {OB} + \overrightarrow {OE} ) + (\overrightarrow {OD} + \overrightarrow {OC} )\) suy ra \(\overrightarrow u \) nằm trên đường thẳng OA.
Tương tự chứng minh \(\overrightarrow u \) nằm trên đường thẳng OB suy ra \(\overrightarrow u \) là véc tơ \(\overrightarrow 0\).
Lời giải chi tiết
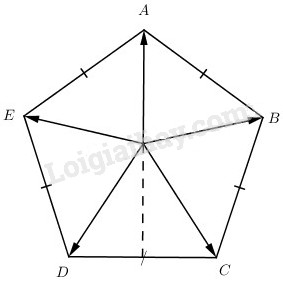
Đặt \(\overrightarrow u = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {OE} \).
Ta có thể viết:
\(\overrightarrow u = \overrightarrow {OA} + (\overrightarrow {OB} + \overrightarrow {OE} ) + (\overrightarrow {OD} + \overrightarrow {OC} )\).
Vì \(OA\) là phân giác của góc \(BOE\) và \(OE = OB\) nên tổng \(\overrightarrow {OB} + \overrightarrow {OE} \) là một vec tơ nằm trên đường thẳng \(OA\).
Tương tự, vec tơ tổng \(\overrightarrow {OC} + \overrightarrow {OD} \) là một vec tơ cũng nằm trên đường thẳng \(OA\).
Vậy \(\overrightarrow u \) là một vec tơ nằm trên đường thẳng \(OA\).
Chứng minh hoàn toàn tương tự, ta có \(\overrightarrow u \) cũng là một vec tơ nằm trên đường thẳng \(OB\).
Từ đó suy ra \(\overrightarrow u \) phải là vec tơ – không: \(\overrightarrow u = \overrightarrow 0 \).
Bài toán trong trường hợp n-giác đều:
Nếu \(A_1A_2…A_n\) là n-giác đều tâm \(O\) thì \(\overrightarrow {O{A_1}} + \overrightarrow {O{A_2}} + ... + \overrightarrow {O{A_n}} = \overrightarrow 0 \).
dapandethi.vn
