Đề bài
Cho tam giác ABC nội tiếp trong đường tròn (O). Gọi H là trực tâm tam giác ABC và B’ là điểm đối xứng với B qua tâm O. Hãy so sánh các vec tơ \(\overrightarrow {AH} \) và \(\overrightarrow {B'C} \), \(\overrightarrow {AB'} \) và \(\overrightarrow {HC} \).
Phương pháp giải - Xem chi tiết
Chứng minh AHCB' là hình bình hành.
Lời giải chi tiết
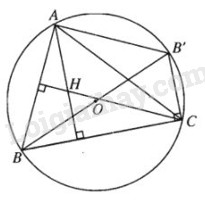
Ta có:
\(\left\{ \begin{array}{l}AH \bot BC\\B'C \bot BC\end{array} \right. \Rightarrow AH//B'C\)
Tương tự \(\left\{ \begin{array}{l}CH \bot AB\\B'A \bot AB\end{array} \right. \Rightarrow CH//B'A\)
Tứ giác AHCB’ có \(AH//B'C,CH//AB'\) nên là hình bình hành.
Suy ra \(\overrightarrow {AH} \) = \(\overrightarrow {B'C} \), \(\overrightarrow {AB'} \) = \(\overrightarrow {HC} \).
dapandethi.vn
