Đề bài
Tính diện tích tam giác cân có cạnh đáy bằng \(a\) và cạnh bên bằng \(b.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Tam giác cân là tam giác có hai cạnh bằng nhau.
- Định lí Pytago: Bình phương cạnh huyền bằng tổng bình phương của hai cạnh góc vuông.
- Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.
Lời giải chi tiết
Gọi \(h\) là chiều cao của tam giác cân có đáy là \(a\) và cạnh bên là \(b.\)
Xét tam giác \(ABC\) cân tại \(A\) có \(AB=b, BC=a\) và chiều cao \(AH=h\). Ta tính diện tích tam giác \(ABC\).
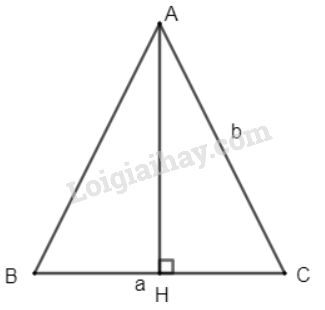
Vì \(\Delta ABC\) cân tại \(A\) (gt) nên \(AH\) vừa là đường cao vừa là đường trung tuyến (tính chất tam giác cân). Suy ra, \(H\) là trung điểm của \(BC\).
\( \Rightarrow BH = \dfrac{{BC}}{2} = \dfrac{a}{2}\)
Áp dụng định lý Pytago vào tam giác vuông \(ABH\) ta có:
\(A{B^2} = A{H^2} + B{H^2}\)
\( \Rightarrow A{H^2} = A{B^2} - B{H^2}\)
\({h^2} = {b^2} - {\left( {\dfrac{a}{2}} \right)^2} = \dfrac{{4{b^2} - {a^2}}}{4} \)\(\Rightarrow h = \dfrac{{\sqrt {4{b^2} - {a^2}} }}{2}\)
Diện tích tam giác \(ABC\) là:
\(S = \dfrac{1}{2}ah = \dfrac{1}{2}a.\dfrac{{\sqrt {4{b^2} - {a^2}} }}{2} \)\(= \dfrac{1}{4}a\sqrt {4{b^2} - {a^2}} .\)
dapandethi.vn
