Đề bài
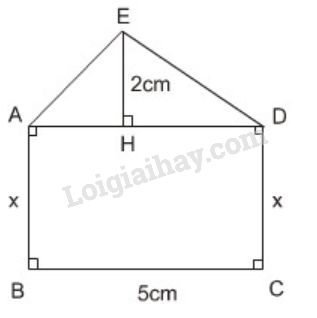
Tính \(x\) sao cho diện tích hình chữ nhật \(ABCD\) gấp \(3\) lần diện tích \(∆ADE\) (h.\(134\))
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng: Công thức tính diện tích tam giác, diện tích hình chữ nhật, biểu diễn diện tích hình chữ nhật theo diện tích của \(∆ADE\).
Lời giải chi tiết
Ta có: \(AD = BC = 5cm\) (vì \(ABCD\) là hình chữ nhật)
Diện tích \(∆ADE\) là: \({S_{ADE}} = \dfrac{{EH.A{\rm{D}}}}{2} = \dfrac{{2.5}}{2} = 5\;(c{m^2})\)
Diện tích hình chữ nhật \(ABCD\) là: \({S_{ABC{\rm{D}}}} = 5{\rm{x}}\left( {c{m^2}} \right)\)
Theo đề bài ta có:
\(\begin{array}{l}
{S_{ABC{\rm{D}}}} = 3{S_{ADE}} \\\Rightarrow 5{\rm{x}} = 3.5 = 15\\
\Rightarrow x = 15:5 = 3cm.
\end{array}\)
Vậy \(x = 3cm.\)
