Đề bài
Cho tam giác \(ABC\). Hãy chỉ ra một số vị trí của điểm \(M\) nằm trong tam giác đó sao cho:
\({S_{AMB}} + {S_{BMC}} = {S_{MAC}}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Kẻ đường cao \(BH, MK.\)
- Áp dụng công thức tính diện tích tam giác: Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.
Lời giải chi tiết
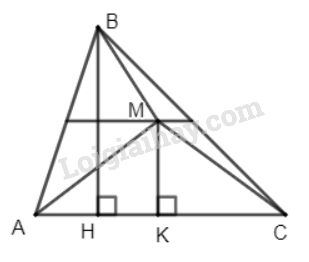
Kẻ đường cao \(BH, MK.\)
Theo giả thiết, \(M\) là điểm nằm trong tam giác \(ABC\) sao cho:
\({S_{AMB}} + {\rm{ }}{S_{BMC}} = {\rm{ }}{S_{MAC}}\) (1)
Ta lại có: \({S_{AMB}} + {S_{BMC}} + {S_{MAC}} = {S_{ABC}}\) (2)
Thay (1) vào (2) ta được: \({S_{MAC}}+ {S_{MAC}}={S_{ABC}}\)
\(\Rightarrow 2.{S_{MAC}} = {S_{ABC}}\)
\(\Rightarrow {S_{MAC}} = \dfrac{1}{2}{S_{ABC}}\)
\(\Rightarrow \dfrac{1}{2}MK.AC = \dfrac{1}{2}\left( {\dfrac{1}{2}BH.AC} \right)\)
\(⇒MK = \dfrac{1}{2}BH\)
Do đó, \(M\) nằm trên đường thẳng thuộc nửa mặt phẳng bờ \(AC\) chứa \(B\) sao cho khoảng cách từ \(M\) đến \(AC\) bằng \(\dfrac{1}{2}\) đường cao \(BH\).
Vậy điểm \(M\) nằm trong tam giác \(ABC\) và nằm trên đường trung bình ứng với cạnh \(AC\) của \(ΔABC\)
dapandethi.vn
