Đề bài
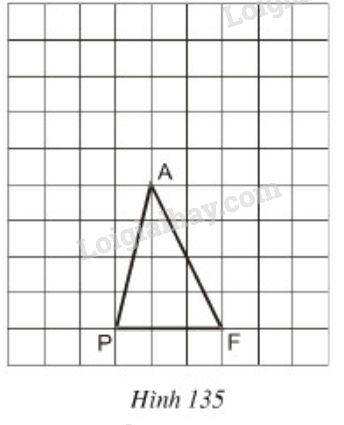
Tam giác \(PAF\) được vẽ trên giấy kẻ ô vuông (h.\(135\)).
Hãy chỉ ra:
a) Một điểm \(I\) sao cho \({S_{PIF}} = {S_{PAF}}\)
b) Một điểm \(O\) sao cho \({S_{POF}} = 2.{S_{PAF}}\)
c) Một điểm \(N\) sao cho \({S_{PNF}} = \dfrac{1}{2}{S_{PAF}}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng
- Cách tính diện tích tam giác.
- Khoảng cách giữa hai đường thẳng song song.
Lời giải chi tiết
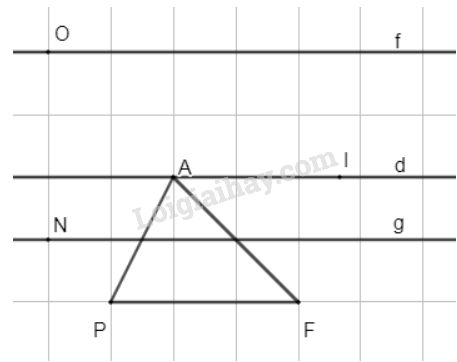
a) Nếu lấy điểm \(I\) bất kì nằm trên đường thẳng \(d\) đi qua \(A\) và song song với đường thẳng \(PF\) thì \({S_{PIF}} = {S_{PAF}}\)
(vì khi đó hai tam giác chung đáy \(PF\) và chiều cao hạ từ \(A\) hay \(I\) xuống \(PF\) đều bằng nhau (\(d // PF\)))
Có vô số điểm \(I\) thỏa mãn yêu cầu bài toán nằm trên đường thẳng \(d\) song song với \(PF\).
b) Nếu lấy một điểm \(O\) sao cho khoảng cách từ \(O\) đến đường thẳng \(PF\) bằng hai lần khoảng cách từ \(A\) đến đường thẳng \(PF\) thì \({S_{POF}} = 2.{S_{PAF}}\)
(vì khi đó hai tam giác chung đáy \(PF\) và chiều cao hạ từ \(O\) xuống \(PF\) bằng \(2\) lần chiều cao hạ từ \(A\) xuống \(PF\))
Có vô số điểm \(O\) thỏa mãn yêu cầu bài toán nằm trên đường thẳng \(f\) song song với \(PF\).
c) Nếu lấy điểm \(N\) sao cho khoảng cách từ \(N\) đến đường thẳng \(PF\) bằng \(\dfrac{1}{2}\) khoảng cách từ \(A\) đến \(PF\) thì \({S_{PNF}} = \dfrac{1}{2}{S_{PAF}}\)
(vì khi đó hai tam giác chung đáy \(PF\) và chiều cao hạ từ \(N\) xuống \(PF\) bằng \(\dfrac{1}{2}\) chiều cao hạ từ \(A\) xuống \(PF\))
Có vô số điểm \(N\) như thế nằm trên đường thẳng \(g\) song song với \(PF.\)
dapandethi.vn
