Đề bài
Câu 1. Đúng ghi Đ, sai ghi S vào ô trống:
Tính:
|
a) \(\dfrac{3}{7} + \dfrac{8}{{21}} = \dfrac{{17}}{{21}}\) |
|
|
b) \(\dfrac{4}{5} - \dfrac{2}{3} = \dfrac{2}{{15}}\) |
|
|
c) \(\dfrac{7}{{11}} \times \dfrac{3}{{11}} = \dfrac{{21}}{{11}}\) |
|
|
d) \(\dfrac{1}{3}:\dfrac{1}{4} = \dfrac{4}{3}\) |
|
Câu 2. Khoanh vào chữ đặt trước câu trả lời đúng:
Tổng số tuổi của hai mẹ con hiện nay là 36 tuổi. Tuổi con bằng \(\dfrac{2}{7}\) tuổi mẹ. Tính tuổi mẹ hiện nay.
A) 28 tuổi
B) 22 tuổi
C) 26 tuổi
Câu 3. Đúng ghi Đ, sai ghi S vào ô trống:
Trên bản đồ tỉ lệ 1: 4000, chiều dài sân trường đo được 4cm. Hỏi chiều dài thật của sân trường là bao nhiêu mét?
|
a) 16m |
|
|
b) 160m |
|
|
c) 1600m |
|
Câu 4. Khoanh vào chữ cái đặt trước câu trả lời đúng:
Một chiếc cầu dài 800m. Trên bản đồ tỉ lệ 1 : 40 000, người ta vẽ trên bản đồ chiếc cầu đó dài bao nhiêu xăng-ti-mét?
A) 200cm
B) 20cm
C) 2cm
Câu 5. Đúng ghi Đ, sai ghi S vào ô trống:
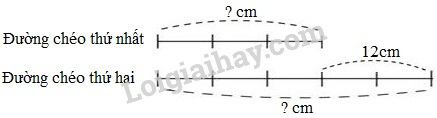
Hiệu độ dài hai đường chéo của một hình thoi là 12cm, tỉ số hai đường chéo là \(\dfrac{3}{5}\). Tính diện tích hình thoi đó.
|
a) 270cm2 |
|
|
b) 300cm2 |
|
|
c) 540cm2 |
|
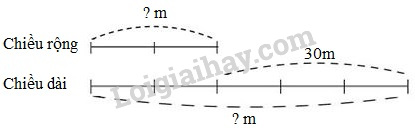
Câu 6. Một mảnh vườn hình chữ nhật, nếu bớt chiều dài đi 18m, thêm vào chiều rộng 12m thì mảnh vườn trở thành hình vuông. Tính diện tích mảnh vườn đó, biết tỉ số giữa chiều rộng và chiều dài mảnh vườn là \(\dfrac{2}{5}\).
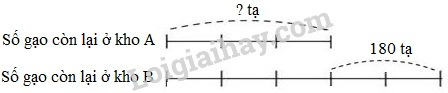
Câu 7. Kho B có nhiều hơn kho A là 180 tạ gạo. Nếu mỗi kho bớt đi 400 tạ thì số gạo còn lại ở kho A bằng \(\dfrac{3}{5}\) số gạo còn lại ở kho B. Tính số gạo lúc đầu ở mỗi kho?
Lời giải chi tiết
Câu 1.
Phương pháp:
- Muố cộng (hoặc trừ) hai phân số ta quy đồng mẫu số các phân số rồi cộng (hoặc trừ) hai phân số sau khi quy đồng.
- Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
- Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.
Cách giải:
Ta có:
a) \(\dfrac{3}{7} + \dfrac{8}{{21}} = \dfrac{{3 \times 3}}{{7 \times 3}} + \dfrac{8}{{21}}\)\( = \dfrac{9}{{21}} + \dfrac{8}{{21}} = \dfrac{{17}}{{21}}\)
b) \(\dfrac{4}{5} - \dfrac{2}{3} = \dfrac{{4 \times 3}}{{5 \times 3}} - \dfrac{{2 \times 5}}{{3 \times 5}}\)\( = \dfrac{{12}}{{15}} - \dfrac{{10}}{{15}} = \dfrac{2}{{15}}\)
c) \(\dfrac{7}{{11}} \times \dfrac{3}{{11}} = \dfrac{{7 \times 3}}{{11 \times 11}} = \dfrac{{21}}{{121}}\)
d) \(\dfrac{1}{3}:\dfrac{1}{4} = \dfrac{1}{3} \times \dfrac{4}{1} = \dfrac{4}{3}\).
Vậy ta có bảng kết quả như sau:
|
a) \(\dfrac{3}{7} + \dfrac{8}{{21}} = \dfrac{{17}}{{21}}\) |
Đ |
|
b) \(\dfrac{4}{5} - \dfrac{2}{3} = \dfrac{2}{{15}}\) |
Đ |
|
c) \(\dfrac{7}{{11}} \times \dfrac{3}{{11}} = \dfrac{{21}}{{11}}\) |
S |
|
d) \(\dfrac{1}{3}:\dfrac{1}{4} = \dfrac{4}{3}\) |
Đ |
Câu 2. Khoanh vào chữ đặt trước câu trả lời đúng:
Tổng số tuổi của hai mẹ con hiện nay là 36 tuổi. Tuổi con bằng \(\dfrac{2}{7}\) tuổi mẹ. Tính tuổi mẹ hiện nay.
Phương pháp:
Tìm tuổi mẹ hiện nay theo dạng toán tìm hai số khi biết tổng và tỉ số của hai số đó.
Cách giải:
Ta có sơ đồ:
Tổng số phần bằng nhau là:
\(2 + 7 = 9\) (phần)
Tuổi mẹ hiện nay là:
\(36:9 \times 7 = 28\) (tuổi)
Chọn A. 28 tuổi
Câu 3.
Phương pháp:
Với bản đồ tỉ lệ \(1 : 4000\), muốn tìm chiều dài thật của sân trường ta lấy độ dài trên bản đồ nhân với \(4000\), sau đó đổi kết quả sang đơn vị đo là mét.
Cách giải:
Chiều dài thật của sân trường là:
\(4000 \times 4 = 16000\;(cm)\)
\(16 000cm = 160m\)
Ta có bảng đáp án sau:
|
a) \(16m\) |
S |
|
b) \(160m\) |
Đ |
|
c) \(1600m\) |
S |
Câu 4.
Phương pháp:
- Đổi số đo độ dài chiếc cầu sang số đo có đơn vị là xăng-ti-mét.
- Với bản đổ tỉ lệ \(1 : 40 000\), muốn tìm độ dài của chiếc cầu đó trên bản đồ ta lấy chiều dài thực tế của chiếc cầu (với đơn vị đo là xăng-ti-mét) chia cho \(40 000\).
Cách giải:
Đổi \(800m = 80 000cm\).
Trên bản đồ chiếc cầu dài số xăng-ti-mét là:
\(80000:40000 = 2\;(cm)\)
Chọn C. 2cm
Câu 5.
Phương pháp:
- Tìm độ dài hai đường chéo hình thoi theo dạng toán tìm hai số khi biết hiệu và tỉ số của hai số đó.
- Muốn tính diện tích hình thoi ta lấy tích độ dài hai đường chéo chia cho \(2\).
Cách giải:
Ta có sơ đồ:
Hiệu số phần bằng nhau là:
\(5 - 3 = 2\) (phần)
Đường chéo thứ nhất của hình thoi dài là:
\(12:2 \times 3 = 18\;(cm)\)
Đường chéo thứ hai của hình thoi dài là:
\(18 + 12 = 30\;(cm)\)
Diện tích hình thoi là:
\(\left( {18 \times 30} \right):2 = 270\;(cm^2)\)
Ta có bảng kết quả sau:
|
a) \(270cm^2\) |
Đ |
|
b) \(300cm^2\) |
S |
|
c) \(540cm^2\) |
S |
Câu 6.
Phương pháp:
- Tìm hiệu giữa chiều dài và chiều rộng:
Vì chiều dài bớt đi \(18m\), chiều rộng thêm vào \(12m\) thì mảnh vườn trở thành hình vuông nên hiệu giữa chiều dài và chiều rộng là \(18 + 12 = 30m\).
- Tìm chiều dài và chiều rộng theo dạng toán tìm hai số khi biết hiệu và tỉ số của hai số đó.
- Tính diện tích = chiều dài \(\times \) chiều rộng.
Cách giải:
Chiều dài hơn chiều rộng số mét là:
\(18 + 12 = 30\;(m)\)
Ta có sơ đồ:
Hiệu số phần bằng nhau là:
\(5 - 2 = 3\) (phần)
Chiều rộng mảnh vườn là:
\(30:3 \times 2 = 20\;(m)\)
Chiều dài mảnh vườn là:
\(20 + 30 = 50\;(m)\)
Diện tích mảnh vườn là:
\(20 \times 50 = 1000\;(m^2)\)
Đáp số: \(1000m^2 \).
Câu 7.
Phương pháp:
- Nếu mỗi kho cùng bớt đi \(400\) tạ gạo thì hiệu số gạo hai kho không đổi và bằng \(180\) tạ.
- Ta tìm số gạo còn lại của mỗi kho theo dạng toán tìm hai số khi biết hiệu và tỉ số của hai số đó.
- Tìm số gạo lúc đầu đầu của mỗi kho ta lấy số gạo còn lại cộng với số gạo đã lấy ra.
Cách giải:
Nếu mỗi kho cùng bớt đi \(400\) tạ gạo thì hiệu số gạo hai kho không đổi và bằng \(180\) tạ.
Ta có sơ đồ:
Hiệu số phần bằng nhau là:
\(5 - 3 = 2\) (phần)
Số gạo ở kho A sau khi bớt đi 400 tạ gạo là:
\(180:2 \times 3 = 270\) (tạ)
Lúc đầu kho A có số gạo là:
\(270 + 400 = 670\) (tạ)
Lúc đầu kho B có số gạo là:
\(670 + 180 = 850\) (tạ)
Đáp số: Kho A: \(670\) tạ;
Kho B: \(850\) tạ.
dapandethi.vn