Đề bài
Phần 1. Trắc nghiệm (3 điểm)
Khoanh vào chữ đặt trước câu trả lời đúng
Câu 1. Cho các số: 1250; 2370; 4725; 3960. Số chia hết cho 2; 3; 5 và 9 là:
A. 1250 B. 2370
C. 4725 D. 3960
Câu 2. Số thích hợp điền vào chỗ chấm để 30m2 3dm2 = … dm2 là:
A. 300 300dm2 B. 30300dm2
C. 3300dm2 D. 3003dm2
Câu 3. Phân số \(\dfrac{5}{6}\) bằng phân số nào dưới đây:
A. \(\dfrac{{20}}{{18}}\) B. \(\dfrac{{20}}{{24}}\)
C. \(\dfrac{{24}}{{20}}\) D. \(\dfrac{{18}}{{20}}\)
Câu 4. Một đội công nhân đắp một quãng đường dài 180m. Sau một ngày đắp được \(\dfrac{4}{5}\) quãng đường. Hỏi còn lại bao nhiêu mét quãng đường chưa đắp?
A. 20m B. 30m
C. 36m D. 40m
Câu 5. Tìm \(\dfrac{2}{5}\) của 140kg.
A. 56kg B. 58kg
C. 60kg D. 62kg
Câu 6. Trên bản đồ tỉ lệ 1 : 200, chiều dài phòng học lớp em đo được 5cm. Chiều dài thật của phòng học đó là:
A. 500cm B. 1000cm
C. 10 000cm D. 700cm
Phần 2. Tự luận (7 điểm)
Bài 1. Tính:
\(a)\,\,\dfrac{2}{5} + \dfrac{3}{4}\) \(b)\dfrac{3}{2} - \dfrac{5}{8}\)
\(c)\,\,\dfrac{3}{7} \times \dfrac{4}{5}\) \(d)\,\,\dfrac{2}{5}:\dfrac{2}{3}\)
Bài 2. Tìm \(x\), biết :
\(a)\; \dfrac{7}{{10}} \times x = \dfrac{1}{2}\).
\(b)\; x:\dfrac{5}{8} = \dfrac{4}{{15}}\).
Bài 3. Một thửa ruộng hình chữ nhật có nửa chu vi là 136 m, biết chiều dài bằng \(\dfrac{5}{3}\) chiều rộng.
a) Tính diện tích của thửa ruộng.
b) Người ta trồng lúa trên thửa ruộng, cứ 1\(m^2\) thì thu được \(\dfrac{3}{5}\)kg thóc. Tính số thóc thu được trên thửa ruộng đó.
Bài 4. Tính bằng cách thuận tiện nhất.
\(3 \times \dfrac{7}{{10}} + \dfrac{7}{{10}} \times 5 + 2 \times \dfrac{7}{{10}}\)
Lời giải chi tiết
Phần 1. Trắc nghiệm
Câu 1.
Phương pháp:
- Các số có chữ số tận cùng là 0 thì chia hết cho cả 2 và 5.
- Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3.
- Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9.
Cách giải:
Số chia hết cho 2; 3; 5 và 9 là 3960.
Chọn D.
Câu 2.
Phương pháp:
Áp dụng cách đổi: 1m2 = 100dm2.
Cách giải:
Ta có: 30m2 3dm2 = 30m2 + 3dm2 = 3000dm2 + 3dm2 = 3003dm2.
Chọn D.
Câu 3.
Phương pháp:
Áp dụng tính chất: Khi nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Cách giải:
Ta có: \(\dfrac{5}{6} = \dfrac{5 \times 4}{6 \times 4}=\dfrac{20}{24}\)
Chọn B.
Câu 4.
Phương pháp:
- Tính quãng đường đã đắp = độ dài cả quãng đường \(\times \,\dfrac{4}{5}\).
- Quãng đường chưa đắp = độ dài cả quãng đường \(-\) quãng đường đã đắp.
Cách giải:
Một ngày đội công nhân đắp được quãng đường là:
180 × \(\dfrac{4}{5}\) = 144 (m)
Còn lại số mét đường chưa đắp là:
180 - 144 = 36 (m)
Đáp số: 36m.
Chọn C.
Câu 5.
Phương pháp:
Muốn tìm \(\dfrac{2}{5}\) của 140kg ta lấy 140 nhân với \(\dfrac{2}{5}\), sau đó ghi thêm đơn vị vào kết quả.
Cách giải:
\(\dfrac{2}{5}\) của 140kg là
\(140 \times \frac{2}{5} = 56\) (kg)
Đáp số: 56kg.
Chọn A.
Câu 6.
Phương pháp:
Muốn tìm độ dài thật của phòng học đó ta lấy độ dài trên bản đồ nhân với 200.
Cách giải:
Chiều dài thật của phòng học đó là:
5 × 200 = 1000 (cm)
Đáp số: 1000cm.
Chọn B
Phần 2. Tự luận
Bài 1.
Phương pháp:
- Muốn cộng hoặc trừ hai phân số ta quy đồng mẫu số hai phân số rồi cộng hoặc trừ hai phân số đó.
- Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
- Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.
Cách giải:
\(a)\,\,\dfrac{2}{5} + \dfrac{3}{4} = \dfrac{8}{{20}} + \dfrac{{15}}{{20}} = \dfrac{{23}}{{20}}\)
\(b)\dfrac{3}{2} - \dfrac{5}{8} = \dfrac{{12}}{8} - \dfrac{5}{8} = \dfrac{7}{8}\)
\(c)\,\,\dfrac{3}{7} \times \dfrac{4}{5} = \dfrac{{3 \times 4}}{{7 \times 5}} = \dfrac{{12}}{{35}}\)
\(d)\,\,\dfrac{2}{5}:\dfrac{2}{3} = \dfrac{2}{5} \times \dfrac{3}{2} = \dfrac{6}{{10}} = \dfrac{3}{5}\)
Bài 2.
Phương pháp:
Áp dụng các quy tắc:
- Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.
- Muốn tìm số bị chia ta lấy thương nhân với số chia.
Cách giải:
\(\begin{array}{l}a)\; \dfrac{7}{{10}} \times x = \dfrac{1}{2}\\\,\,\,\,\,\,\,\,\,x = \dfrac{1}{2}:\dfrac{7}{{10}}\\\,\,\,\,\,\,\,\,\,x = \dfrac{1}{2} \times \dfrac{10}{7}\\\,\,\,\,\,\,\,\,\,x = \dfrac{{10}}{{14}} = \dfrac{5}{7}\end{array}\).
\(\begin{array}{l}b)\; x:\dfrac{5}{8} = \dfrac{4}{{15}}\\ \,\,\,\,\,\,\,\,x = \dfrac{4}{{15}} \times \dfrac{5}{8}\\ \,\,\,\,\,\,\,\,x = \dfrac{{20}}{{120}} = \dfrac{1}{6}\end{array}\).
Bài 3.
Phương pháp:
- Vẽ sơ đồ và tìm chiều dài, chiều rộng theo bài toán tìm hai số khi biết tổng và tỉ số của hai số đó.
- Tính diện tích thửa ruộng ta lấy chiều dài nhân với chiều rộng.
- Tính số thóc thu được ta lấy \(\dfrac{3}{5}\)kg nhân với diện tích thửa ruộng.
Cách giải:
a) Ta có sơ đồ:
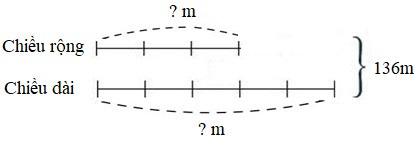
Theo sơ đồ, tổng số phần bằng nhau là:
5 + 3 = 8 (phần)
Chiều dài thửa ruộng hình chữ nhật là:
136: 8 × 5 = 85 (m)
Chiều rộng thửa ruộng hình chữ nhật là:
136 – 85 = 51 (m)
Diện tích thửa ruộng hình chữ nhật là:
85 × 51 = 4335 (m2 )
b) Số thóc thu được trên thửa ruộng đó là:
4335 × \(\dfrac{3}{5}\)= 2601 (kg)
Đáp số: a) 4335m2;
b) 2601kg.
Bài 4.
Phương pháp:
- Áp dụng tính chất giao hoán của phép nhân.
- Áp dụng công thức \(a \times b + a \times c + a \times d = a \times (b+c+d)\).
Cách giải:
\(\begin{array}{l}
3 \times \dfrac{7}{{10}} + \dfrac{7}{{10}} \times 5 + 2 \times \dfrac{7}{{10}}\\
= \dfrac{7}{{10}} \times 3 + \dfrac{7}{{10}} \times 5 + \dfrac{7}{{10}} \times 2\\
= \dfrac{7}{{10}} \times \left( {3 + 5 + 2} \right)\\
= \dfrac{7}{{10}} \times 10\\
= 7
\end{array}\)
dapandethi.vn
