Câu 1.
Tam giác \(ABC\) có \(\widehat A = {70^o};\,\,\widehat B - \widehat C = {50^o}.\) Số đo của góc \(C\) bằng:
\(\begin{array}{l}(A)\,{80^o}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(B)\,{60^o}\\(C)\,{30^o}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(D)\,\,{40^o}\end{array}\)
Phương pháp giải:
Tổng ba góc của một tam giác bằng \(180^o\).
Lời giải chi tiết:
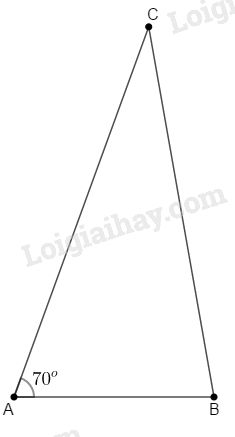
Áp dụng định lí tổng ba góc của một tam giác vào \(\Delta ABC\) ta có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ \Rightarrow \widehat B + \widehat C = {180^o} - \widehat A\\ \Rightarrow \widehat B + \widehat C = {180^o} - {70^o}\\ \Rightarrow \widehat B + \widehat C = {110^o}\,\,\,(1)\end{array}\)
Từ \(\widehat B - \widehat C = {50^o} \Rightarrow \widehat B = \widehat C + {50^o}\) thay vào (1) ta được:
\(\begin{array}{l}\widehat C + {50^o} + \widehat C = {110^o}\\ \Rightarrow 2\widehat C + {50^o} = {110^o}\\ \Rightarrow 2\widehat C = {110^o} - {50^o} = {60^o}\\ \Rightarrow \widehat C = {60^o}:2 = {30^o}\end{array}\)
Chọn C.
Câu 2.
Tam giác \(ABC\) vuông tại \(B\) có \(\widehat A = 3\widehat C.\) Số đo của góc \(A\) bằng:
\(\begin{array}{l}(A)\,22,{5^o}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(B)\,67,{5^o}\\(C)\,{60^o}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(D)\,{90^o}\end{array}\)
Phương pháp giải:
Trong tam giác vuông hai góc nhọn phụ nhau.
Lời giải chi tiết:
Tam giác \(ABC\) vuông tại \(B\) nên \(\widehat A + \widehat C = {90^o}\,\,\,(1)\)
Thay \(\widehat A = 3\widehat C\) vào (1) ta được:
\(\begin{array}{l}3\widehat C + \widehat C = {90^o}\\ \Rightarrow 4\widehat C = {90^o}\\ \Rightarrow \widehat C = {90^o}:4 = 22,{5^o}\\ \Rightarrow \widehat A = 3\widehat C = 3.22,5 = 67,{5^o}\end{array}\)
Chọn B.
Câu 3.
Đúng ghi Đ, sai ghi S vào ô trống trong mỗi khẳng định sau
a) Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì cặp góc còn lại bằng nhau.
b) Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì cặp góc nhọn còn lại bằng nhau.
c) Góc ngoài của một tam giác bao giờ cũng là góc tù.
Phương pháp giải:
a) Tổng ba góc của một tam giác bằng \(180^o\).
b) Trong tam giác vuông hai góc nhọn phụ nhau.
c) Đưa ra ví dụ cụ thể.
Lời giải chi tiết:
a) Đ
\(\Delta ABC\) và \(\Delta A'B'C'\) có \(\widehat A = \widehat {A'};\,\,\widehat B = \widehat {B'}\,\,\,\,\,(\,1\,)\)
Theo định lí tổng ba góc của một tam giác ta có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\,\,\,\,\,\,(2)\\\widehat {A'} + \widehat {B'} + \widehat {C'} = {180^o}\,\,(3)\end{array}\)
Từ (1), (2) và (3) suy ra \(\widehat C = \widehat {C'}.\)
b) Đ
Xét tam giác \(ABC\) vuông tại \(A\); tam giác \(A’B’C’\) vuông tại \(A’\); trong đó \(\widehat B = \widehat {B'}\,\,\,(4)\)
Do đó ta có:
\(\begin{array}{l}\widehat B + \widehat C = {90^o}\,\,\,\,\,(5)\\\,\widehat {B'} + \widehat {C'} = {90^o}\,\,(6)\end{array}\)
Từ (4), (5) và (6) suy ra \(\widehat C = \widehat {C'}.\)
c) S
Ví dụ: \(\Delta ABC\) có \(\widehat A = {120^o}\)
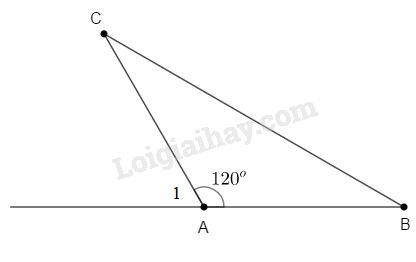
Góc ngoài tại \(A\) là \(\widehat {{A_1}} = {180^o} - {120^o} = {60^o}\)
Do đó \(\widehat {{A_1}}\) là góc nhọn.
dapandethi.vn
