Đề bài
Cho tam giác \(ABC\): \(\widehat{B}= 80^0\), \(\widehat{C}= 30^0\). Tia phân giác của góc \(A\) cắt \(BC\) ở \(D\). Tính \(\widehat{ADC},\widehat{ADB}\).
Phương pháp giải - Xem chi tiết
Áp dụng định lí:
- Tổng ba góc của một tam giác bằng \({180^0}\);
- Hai góc kề bù có tổng số đo bằng \({180^0}\).
Lời giải chi tiết
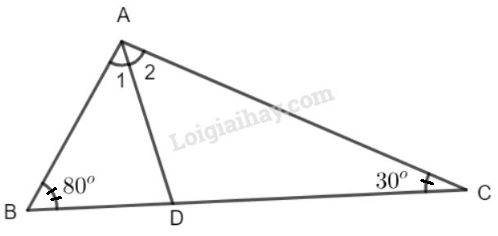
Xét \(\Delta ABC\) ta có: \(\widehat {A} + \widehat B + \widehat C = {180^0}\)
\(\widehat{A}= 180^0- \widehat{B}-\widehat{C}\) \(= 180^0- 80^0- 30^0= 70^0\)
\(AD\) là tia phân giác của góc \(A\) nên
\(\widehat{A_{1}}=\widehat{A_{2}}=\dfrac{\widehat{A}}2=\dfrac{70^{0}}2= 35^0\)
Xét \(\Delta ADC\), ta có \(\widehat {ADC} = {180^o} - \widehat {{A_2}} - \widehat C \)\(\,= {180^o} - {35^o} - {30^o} = {115^o}\)
\(\widehat{ADB}= 180^0- \widehat{ADC}= 180^0-115^0\)\(=65^0\).
dapandethi.vn
