Đề bài
Cho tam giác \(ABC\) có \(\widehat{B}=\widehat{C}= 40^0\). Gọi \(Ax\) là tia phân giác của góc ngoài ở đỉnh \(A\). Hãy chứng tỏ \(Ax// BC\).
Phương pháp giải - Xem chi tiết
Áp dụng:
- Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.
- Chứng minh hai đường thẳng song song ta chứng minh cặp góc so le trong bằng nhau.
Lời giải chi tiết
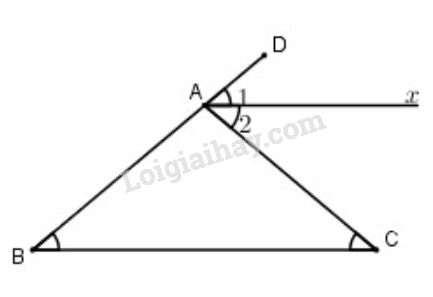
Góc \(CAD \) là góc ngoài của \(\Delta ABC\) nên
\(\widehat{CAD } = \widehat{B}+ \widehat{C}\)\(\,= 40^0+ 40^0=80^0\)
\(Ax\) là tia phân giác góc \({CAD }\) nên
\(\widehat{A_{2} }= \dfrac{1}2\widehat{CAD}=\dfrac{80}2=40^0\)
Hai góc so le trong \( \widehat {{A_2}}\) và \(\widehat{C }\) bằng nhau nên \(Ax// BC\).
dapandethi.vn
