Đề bài
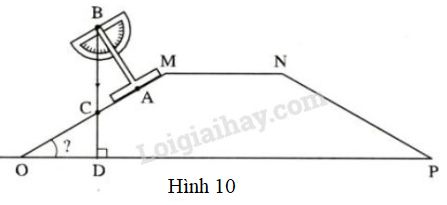
Hình \(10\) biểu diễn mặt cắt ngang của một con đê để đo góc nhọn \(MOP\) tạo bởi mặt phẳng nghiêng của con đê với phương nằm ngang, người ta dùng thước chữ \(T\) và đặt như hình vẽ (\(OA\perp AB\)). Tính góc \(MOP\), biết rằng dây dọi \(BC\) tạo với trục \(BA\) một góc \(\widehat{ABC }= 32^0\)
Phương pháp giải - Xem chi tiết
Áp dụng:
- Tam giác vuông có hai góc nhọn phụ nhau.
- Hai góc đối đỉnh thì bằng nhau.
Lời giải chi tiết
Tam giác \( ABC\) vuông tại \(A\) nên \(\widehat{ABC}+ \widehat{ACB}= 90^0\)(1)
Tam giác \( DOC\) vuông tại \(D\) nên \(\widehat{COD}+ \widehat{OCD}= 90^0\)(2)
Ta lại có \( \widehat{ACB}=\widehat{OCD}\) (đối đỉnh)(3)
Từ (1), (2), (3) suy ra \(\widehat{COD}= \widehat{ABC}\). Vậy \(\widehat{MOP}=32^0\)
dapandethi.vn
