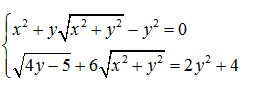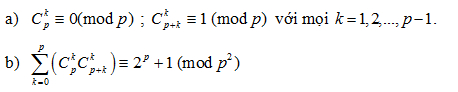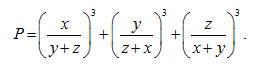Đáp án đề KSCL đầu năm Toán 10 - THPT Chuyên Bắc Ninh - Tổ Toán Tin 2018-2019

Tiếp theo hôm nay chúng ta sẽ cùng nhau khá phá bộ đề kiểm tra khảo sát chất lượng đầu năm môn Toán lớp 10 của trường THPT Chuyên Bắc Ninh. Đây là một trong những bộ đề KSCL đầu năm môn Toán lớp 10 của tổ Toán Tin - THPT chuyên Bắc Ninh.

Và sau đây chúng ta cùng khá phá bộ đề gồm 5 câu và mỗi câu 4 điểm. Bộ đề thi có hướng dẫn giải và đáp án chi tiết xin mời các em cùng xem dưới đây!

Đề KSCL đầu năm 2018-2019 môn Toán lớp 10

Câu 1. Giải hệ phương trình:

Câu 2. Cho  là số nguyên tố lẻ. Chứng minh rằng:

Câu 3.

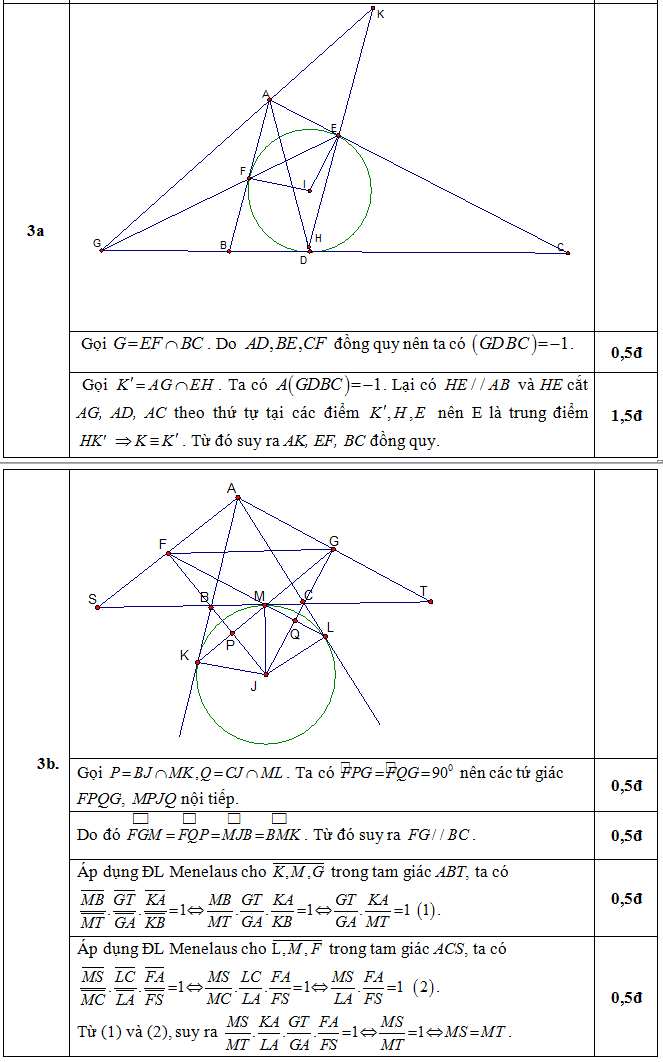
a. Cho tam giác ABC không cân tại A. Đường tròn nội tiếp của tam giác ABC tiếp xúc với các cạnh BC, CA, AB theo thứ tự tại các điểm D, E, F. Đường thẳng qua E và song song với AB cắt AD tại H, gọi K là điểm đối xứng của H qua E. Chứng minh rằng các đường thẳng AK, EF, BC đồng quy.

b. Cho tam giácABC và (J) là đường tròn bàng tiếp gócA của tam giácABC. Đường tròn (J) tiếp xúc với các đường thẳng BC, CA, AB theo thứ tự tại các điểmM, L, K.Hai đường thẳng ML và BJ cắt nhau tại F, hai đường thẳng MK và CJ cắt nhau tại G. Hai đường thẳng AF và AG cắt đường thẳng  BC theo thứ tự tại S và T. Chứng minh rằng , từ đó chứng minh M là trung điểm ST.

Câu 4. Cho các số thực dương x, y, z. Tìm giá trị nhỏ nhất của biểu thức

Câu 5. Trên mặt phẳng, bạn An kẻ  đường thẳng song song nằm ngang vuông góc với  đường thẳng song song nằm dọc và tô màu các giao điểm theo ý định từ trước. Tuy nhiên, An đã tô nhầm màu của   điểm. Để sửa mỗi điểm bị tô sai màu, An cần xóa đi cả đường thẳng chứa điểm đó. Chứng minh rằng, An có thể chọn xóa  đường thẳng ngang và  đường thẳng dọc để sửa được hết tất cả  điểm đã tô nhầm màu.

Hướng dẫn giải đề KSCL đầu năm môn Toán 10

Câu 5:Trong  đường thẳng nằm ngang, ta chọn ra  đường thẳng có số điểm tô nhầm trên mỗi đường là lớn nhất, tức là các đường ngang còn lại có số điểm tô nhầm không lớn hơn các đường ngang đã chọn.

Bây giờ ta chứng minh rằng, số điểm tô nhầm trên  đường này không ít hơn  điểm. Thật vậy, giả sử ngược lại, thì sau khi xóa  đường ngang này, số điểm An cần sửa còn ít nhất +1 điểm. Số này thuộc  đường ngang còn lại, khi đó tất yếu có ít nhất 1 đường ngang chứa từ 2 điểm tô sai màu trở lên. Thế thì chứng tỏ mỗi đường trong  đường ngang chọn ban đầu đều có từ 2 điểm tô sai màu trở lên. Vậy thì số điểm đã xóa không nhỏ hơn  (mâu thuẫn với giả sử trên).

Vậy sau khi xóa n đường ngang thì số điểm tô sai còn lại không vượt quá . Số điểm này nằm trên nhiều nhất  đường dọc. An hoàn toàn chọn được  đường dọc chứa đủ số điểm tô sai còn lại. (đpcm).