Cho hàm số \(y = {x^2} - 4x + 1\)
LG a
Khảo sát và vẽ đồ thị (P) hàm số đã cho.
Lời giải chi tiết:
Hàm số \(y = {x^2} - 4x + 1\) nghịch biến trên khoảng \(\left( { - \infty ;2} \right)\); đồng biến trên khoảng \(\left( {2; + \infty } \right)\)
Đồ thị hàm số:
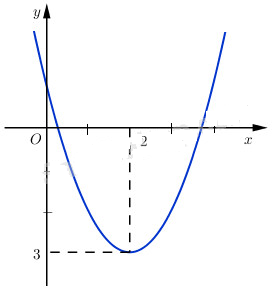
LG b
Gọi (d) là đường thẳng song song với đường phân giác của góc phần tư (I) và đi qua điểm M(0; m). Xác định biểu thức của hàm số có đồ thị (d).
Lời giải chi tiết:
Hàm số cần tìm là \(y = x + m\) .
LG c
Tìm hoành độ các giao điểm A và B (nếu có) của (d) và (P), và tọa độ trung điểm của đoạn thẳng AB (khi A và B phân biệt).
Lời giải chi tiết:
Hoành độ giao điểm của (d) và (P) là nghiệm của phương trình
\({x^2} - 4x + 1 = x + m,\)
Hay \({x^2} - 5x + 1 - m = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
Phương trình (1) có biệt thức \(\Delta = 25 - 4\left( {1 - m} \right) = 21 + 4m\).
Do đó, nếu \(21 + 4m \ge 0\) thì nó có hai nghiệm
\({x_1} = \dfrac{{5 - \sqrt {21 + 4m} }}{2}\) và \({x_2} = \dfrac{{5 + \sqrt {21 + 4m} }}{2}\)
Đó cũng là hoành độ các giao điểm A và B của (d) và (P).
Tọa độ trung điểm của đoạn thẳng AB (khi \(\Delta = 21 + 4m > 0\)) là điểm có tọa độ \(\left( {{x_0};{y_0}} \right)\), trong đó:
\(\begin{array}{l}{x_0} = \dfrac{{{x_1} + {x_2}}}{2} = \dfrac{5}{2};\\{y_0} = {x_0} + m = \dfrac{5}{2} + m.\end{array}\)
dapandethi.vn
