Cho hàm số \(f\left( x \right) = - x + \left| {x + 2} \right| - \left| {x - 2} \right|\).
LG a
Hãy viết hàm số dưới dạng hàm số bậc nhất trên từng khoảng và không chứa dấu giá trị tuyệt đối. (Gọi ý. Xét hàm số trên mỗi khoảng \(\left( { - \infty ; - 2} \right),\left[ { - 2;2} \right)\) và \(\left[ {2; + \infty } \right)\).
Lời giải chi tiết:
\(f\left( x \right) = \left\{ \begin{array}{l} - x - 4\,\,khi\,\,x < - 2\\x\,\,\,\,\,\,\,\,\,\,\,\,\,khi - 2 \le x < 2\\ - x + 4\,\,khi\,\,x \ge 2.\end{array} \right.\)
LG b
Chứng minh rằng \(y = f\left( x \right)\)là hàm số lẻ.
Lời giải chi tiết:
Tập xác định của hàm số là R. Với mọi x, ta có:
Cách 1. (Sử dụng tính chất \(\left| { - a} \right| = \left| a \right|\)):
\(\begin{array}{l}f\left( { - x} \right) = - \left( { - x} \right) + \left| {\left( { - x} \right) + 2} \right| - \left| {\left( { - x} \right) - 2} \right|\\ = x + \left| {x - 2} \right| - \left| {x + 2} \right|\\ = - \left( { - x + \left| {x + 2} \right| - \left| {x - 2} \right|} \right)\\ = - f\left( x \right)\end{array}\)
Cách 2. (Sử dụng kết quả câu a):
- Nếu \(x < - 2\) thì \( - x > 2\), nên \(f\left( { - x} \right) = - \left( { - x} \right) + 4 = - \left( { - x - 4} \right) = - f\left( x \right)\)
- Nếu \( - 2 \le x \le 2\)thì \( - 2 < - x \le 2\), nên \(f\left( { - x} \right) = - x = - f\left( x \right)\)
- Nếu \(x \ge 2\) thì \( - x \le - 2\), nên \(f\left( { - x} \right) = - \left( { - x} \right) - 4 = - \left( { - x + 4} \right) = - f\left( x \right)\).
Vậy trong mọi trường hợp ta đều có \(f\left( { - x} \right) = - f\left( x \right)\), chứng tỏ \(f\left( x \right)\) là số lẻ.
LG c
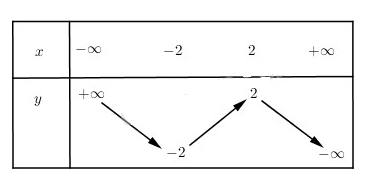
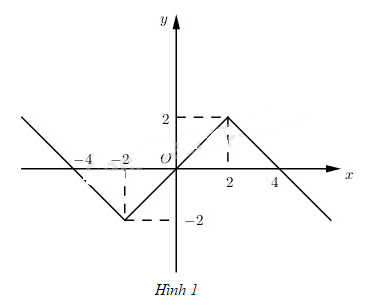
Vẽ đồ thị của hàm số \(y = f\left( x \right)\), lập bảng biến thiên và nêu sự biến thiên của nó trên mỗi khoảng kể trên.
Lời giải chi tiết:
Đồ thị (h.1)
Bảng biến thiên
LG d
Sử dụng đồ thị, hãy tìm các khoảng trên đó hàm số có giá trị dương.
Lời giải chi tiết:
\(\left( { - \infty ; - 4} \right)\) và \(\left( {0;4} \right)\).
dapandethi.vn
