Đề bài
Cho ba dây cung song song \(AA_1, BB_1, CC_1\) của đường tròn \((O)\). Chứng minh rằng trực tâm của ba tam giác \(ABC_1, BCA_1, CAB_1\) nằm trên một đường thẳng.
Lời giải chi tiết
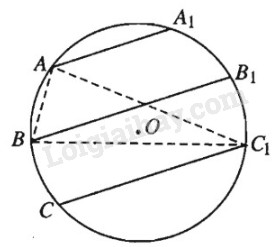
Gọi \(H_1, H_2, H_3\) lần lượt là trực tâm của các tam giác \(ABC_1, BCA_1, CAB_1\). Theo kết quả bài 38, ta có:
\(\begin{array}{l}\overrightarrow {O{H_1}} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {O{C_1}} \,\,\,;\\\overrightarrow {O{H_2}} = \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {O{A_1}} \,\,\,;\\\overrightarrow {O{H_3}} = \overrightarrow {OC} + \overrightarrow {OA} + \overrightarrow {O{B_1}} \,\,.\end{array}\)
Suy ra
\(\begin{array}{l}\overrightarrow {{H_1}{H_2}} = \overrightarrow {O{H_2}} - \overrightarrow {O{H_1}} \\ = \overrightarrow {OC} - \overrightarrow {O{C_1}} + \overrightarrow {O{A_1}} - \overrightarrow {OA}\\ = \overrightarrow {{C_1}C} + \overrightarrow {A{A_1}} \\\overrightarrow {{H_1}{H_3}} = \overrightarrow {O{H_3}} - \overrightarrow {O{H_1}} \\ = \overrightarrow {OC} - \overrightarrow {O{C_1}} + \overrightarrow {O{B_1}} - \overrightarrow {OB} \\ = \overrightarrow {{C_1}C} + \overrightarrow {B{B_1}} .\end{array}\)
Vì các dây cung \(AA_1, BB_1, CC_1\) song song với nhau nên ba vec tơ \(\overrightarrow {A{A_1}} ,\overrightarrow {B{B_1}} ,\overrightarrow {C{C_1}} \) có cùng phương.
Do đó hai vec tơ \(\overrightarrow {{H_1}{H_2}} \) và \(\overrightarrow {{H_1}{H_3}} \) cùng phương , hay ba điểm \(H_1, H_2, H_3\) thẳng hàng.
dapandethi.vn
