Đề bài
Cho điểm \(O\) nằm trong hình bình hành \(ABCD\). Các đường thẳng đi qua \(O\) và song song với các cạnh của hình bình hành lần lượt cắt \(AB, BC, CD, DA\) tại \(M, N, P, Q\). Gọi \(E\) là giao điểm của \(BQ\) và \(DM, F\) là giao điểm của \(BP\) và \(DN\). Tìm điều kiện để \(E, F, O\) thẳng hàng.
Phương pháp giải - Xem chi tiết
Sử dụng kết quả bài tập 19 trang 8 SBT hình học 10 nâng cao:
Cho tam giác \(ABC\). Các điểm \(M, N, P\) lần lượt chia các đoạn thẳng \(AB, BC, CA\) theo các tỉ số lần lượt là \(m, n, p\) (đều khác 1).
Khi đó, \(M, N, P\) thẳng hàng khi và chỉ khi \(mnp=1\) (Định lí Mê-nê-la-uýt)
Lời giải chi tiết
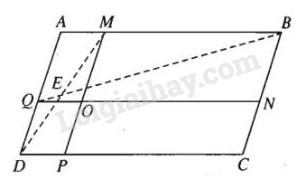
Xét tam giác \(ABQ\) và ba điểm thẳng hàng \(M, E, D\).
Giả sử \(M\) chia \(AB\) theo tỉ số \(m, E\) chia \(BQ\) theo tỉ số \(n, D\) chia \(QA\) theo tỉ số \(p\)
Theo định lí Mê-nê-la-uýt ta có \(mnp=1\).
Xét tam giác \(QNB\) và ba điểm \(O, E, C\).
Khi đó \(O\) chia \(QN\) theo tỉ số \(m,\) \( C\) chia \(NB\) theo tỉ số \(n\) và \(E\) chia \(BQ\) theo tỉ số \(p\).
Vì \(mnp=1\) nên ba điểm \(O, E, C\) thẳng hàng.
Cũng chứng minh tương tự, ta có ba điểm \(F, O, A\) thẳng hàng.
Vậy để ba điểm \(O, E, F\) thẳng hàng, điều kiện cần và đủ là năm điểm \(A, C, E, F, O\) thẳng hàng, hay điểm \(O\) phải nằm trên đường chéo \(AC\) của hình bình hành đã cho.
dapandethi.vn
