Đề bài
Cho tam giác \(ABC\). Đặt \(\overrightarrow {CA} = \overrightarrow a \,;\,\,\overrightarrow {CB} = \overrightarrow b \,\). Lấy các điểm \(A’\) và \(B’\) sao cho \(\overrightarrow {CA'} = m\overrightarrow a \,;\,\,\overrightarrow {CB'} = n\overrightarrow b \,\,\). Gọi \(I\) là giao điểm của \(A’B\) và \(B’A\). Hãy biểu thị vec tơ \(\overrightarrow {CI} \) theo hai vec tơ \(\overrightarrow a \,\) và \(\overrightarrow b \,\).
Lời giải chi tiết
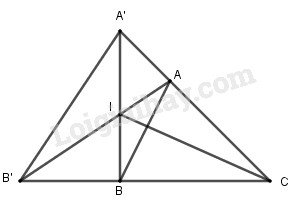
Vì \(I\) nằm trên \(A’B\) và \(AB’\) nên có các số \(x, y\) sao cho:
\(\overrightarrow {CI} = x\overrightarrow {CA'} + (1 - x)\overrightarrow {CB}\)
\( = y\overrightarrow {CA} + (1 - y)\overrightarrow {CB'} \)
hay
\(x.m\overrightarrow a + (1 - x)\overrightarrow b \)
\(= y\overrightarrow a + (1 - y)n\overrightarrow b \).
Vì hai vec tơ \(\overrightarrow a ,\,\overrightarrow b \) không cùng phương nên từ đẳng thức cuối cùng ta suy ra
\(mx = y\) và \((1-x) = n(1-y)\).
Từ đó ta có \(1- x = n(1-mx) = n-mnx\) hay \(x = \dfrac{{1 - n}}{{1 - mn}}\).
Vậy \(\overrightarrow {CI} = \dfrac{{m(1 - n)}}{{1 - mn}}\overrightarrow a + \left( {1 - \dfrac{{1 - n}}{{1 - mn}}} \right)\overrightarrow b \)
\(= \dfrac{{m(1 - n)}}{{1 - mn}}\overrightarrow a + \dfrac{{n(1 - m)}}{{1 - mn}}\overrightarrow b .\)
dapandethi.vn
