Video hướng dẫn giải
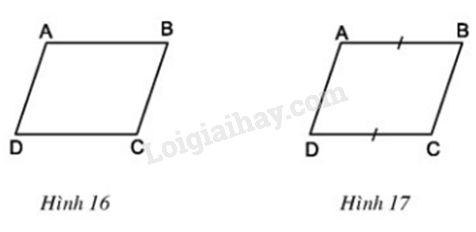
Hình thang \(ABCD\) có đáy \(AB, CD.\)
LG a.
Cho biết \(AD // BC\) (h.16). Chứng minh rằng \(AD = BC, AB = CD.\)
Phương pháp giải:
Áp dụng:
- Xét hai tam giác bằng nhau
- Hai đường thẳng song song thì có cặp góc so le trong bằng nhau.
Lời giải chi tiết:
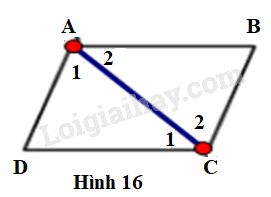
Hình thang \(ABCD\) có đáy \(AB,\,\,CD \Rightarrow AB//CD \Rightarrow \widehat {{A_2}} = \widehat {{C_1}}\) (hai góc so le trong)
Lại có: \(AD // BC\) \( \Rightarrow \widehat {{A_1}} = \widehat {{C_2}}\) (hai góc so le trong)
Xét \(ΔABC\) và \(ΔCDA\) có:
+) \(\widehat {{A_2}} = \widehat {{C_1}}\) (chứng minh trên)
+) \(AC\) chung
+) \(\widehat {{A_1}} = \widehat {{C_2}}\) (chứng minh trên)
\( \Rightarrow ΔABC = ΔCDA\) (g.c.g)
\( \Rightarrow AD = BC, AB = CD\) (các cặp cạnh tương ứng)
LG b.
Cho biết \(AB = CD\) (h.17). Chứng minh rằng \(AD // BC, AD = BC.\)
Phương pháp giải:
Áp dụng:
- Xét hai tam giác bằng nhau
- Hai đường thẳng song song nếu có cặp góc so le trong bằng nhau.
Lời giải chi tiết:
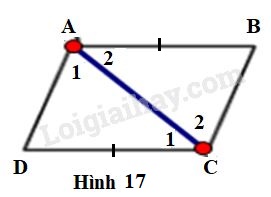
Hình thang \(ABCD\) có đáy \(AB,\,\,CD \Rightarrow AB//CD \Rightarrow \widehat {{A_2}} = \widehat {{C_1}}\) (hai góc so le trong)
Xét \(ΔABC\) và \(ΔCDA\) có:
+) \(AC\) chung
+) \(\widehat {{A_2}} = \widehat {{C_1}}\) (chứng minh trên)
+) \(AB = CD\) (giả thiết)
\( \Rightarrow ΔABC = ΔCDA\) (c.g.c)
\( \Rightarrow AD = BC \) (hai cạnh tương ứng)
\(\widehat {{A_1}} = \widehat {{C_2}}\) (hai góc tương ứng)
Mặt khác \(\widehat {{A_1}} ;\, \widehat {{C_2}}\) ở vị trí so le trong.
\( \Rightarrow AD // BC\) ( Dấu hiệu nhận biết 2 đường thẳng song song)
