Đề bài
Cho hình thang ABCD \(\left( {AB// CD} \right)\) trong đó hai đường phân giác của góc A và B cắt nhau tại điểm K thuộc đáy CD. Chứng minh rằng tổng hai cạnh bên bằng cạnh đáy CD của hình thang.
Phương pháp giải - Xem chi tiết
Sử dụng: Trong tam giác cân, hai góc ở đáy bằng nhau, hai cạnh bên bằng nhau.
Lời giải chi tiết
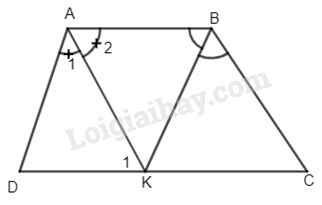
\(AB//CD\,(gt) \Rightarrow \widehat {{A_2}} = \widehat {{K_1}}\) (so le trong(
Mà \(\widehat {{A_1}} = \widehat {{A_2}}\) (do AK là phân giác góc BAD)
\( \Rightarrow \widehat {{A_1}} = \widehat {{K_1}}\) nên \(\Delta ADK\) cân tại D
\( \Rightarrow DA = DK\)
\(AB//CD\,(gt) \Rightarrow \widehat {{ABK}} = \widehat {{BKC}}\) (so le trong(
Mà \(\widehat {{ABK}} = \widehat {{CBK}}\) (do BK là phân giác góc CBA)
\( \Rightarrow \widehat {{KBC}} = \widehat {{BKC}}\) nên \(\Delta BCK\) cân tại C
\( \Rightarrow CB = CK\) mà \(DK + CK = CD\)
\( \Rightarrow DA + CB = CD\)
dapandethi.vn
